逐步回归是一种线性回归模型自变数选择方法，其基本思想是将变数一个一个引入，引入的条件是其偏回归平方和经验是显着的。同时，每引入一个新变数后，对已入选回归模型的老变数逐个进行检验，将经检验认为不显着的变数删除，以保证所得自变数子集中每一个变数都是显着的。此过程经过若干步直到不能再引入新变数为止。这时回归模型中所有变数对因变数都是显着的。

逐步回归法选择变数的过程包含两个基本步骤：一是从回归模型中剔出经检验不显着的变数，二是引入新变数到回归模型中，常用的逐步型选元法有向前法和向后法。

向前法：向前法的思想是变数由少到多，每次增加一个，直至没有可引入的变数为止。具体步骤如下。

步骤1:对 p 个回归自变数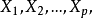 分别同因变数 Y 建立一元回归模型

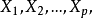
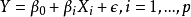
计算变数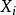 ，相应的回归係数的 F 检验统计量的值，记为 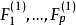,取其中的最大值 ，即

对给定的显着性水平 ，记相应的临界值为 ， ，则将 引入回归模型，记 为选入变数指标集合。

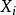
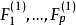
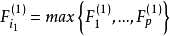
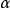
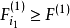
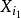
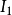
步骤2:建立因变数 Y 与自变数子集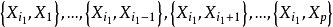 的二元回归模型（即此回归模型的回归元为二元的），共有 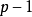个。计算变数的回归係数 F 检验的统计量值，记为 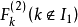，选其中最大者，记为 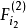,对应自变数脚标记为 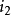，即

。

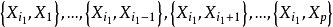
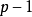
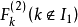
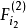
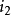
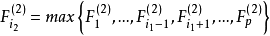
对给定的显着性水平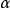 ，记相应的临界值为 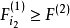， 则变数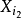 引入回归模型。否则，终止变数引入过程。

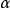
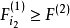
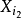
步骤3:考虑因变数对变数子集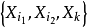 的回归重複步骤2。

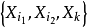
依此方法重複进行，每次从未引入回归模型的自变数中选取一个，知道经检验没有变数引入为止。

向后法与向前法正好相反，它事先将全部自变数选入回归模型，任何逐个剔除对残差平方和贡献较小的自变数。

逐步回归分析的实施过程是每一步都要对已引入回归方程的变数计算其偏回归平方和（即贡献），然后选一个偏回归平方和最小的变数，在预先给定的水平下进行显着性检验，若显着则该变数不必从回归方程中剔除，这时方程中其他几个变数也都不需要剔除（因为其他几个变数的偏回归平方和都大于最小的一个更不需要剔除）。相反，如果不显着，则该变数需要剔除，然后按偏回归平方和由小到大地依次对方程中其他变数进行检验。将对影响不显着的变数全部剔除，保留的都是显着的。接着再对未引入回归方程中的变数分别计算其偏回归平方和，并选其中偏回归方程和最大的一个变数，同样在给定水平下作显着性检验，如果显着则将该变数引入回归方程，这一过程一直持续下去，直到在回归方程中的变数都不能剔除而又无新变数可以引入时为止，这时逐步回归过程结束。