读书笔记摘抄新闻资讯
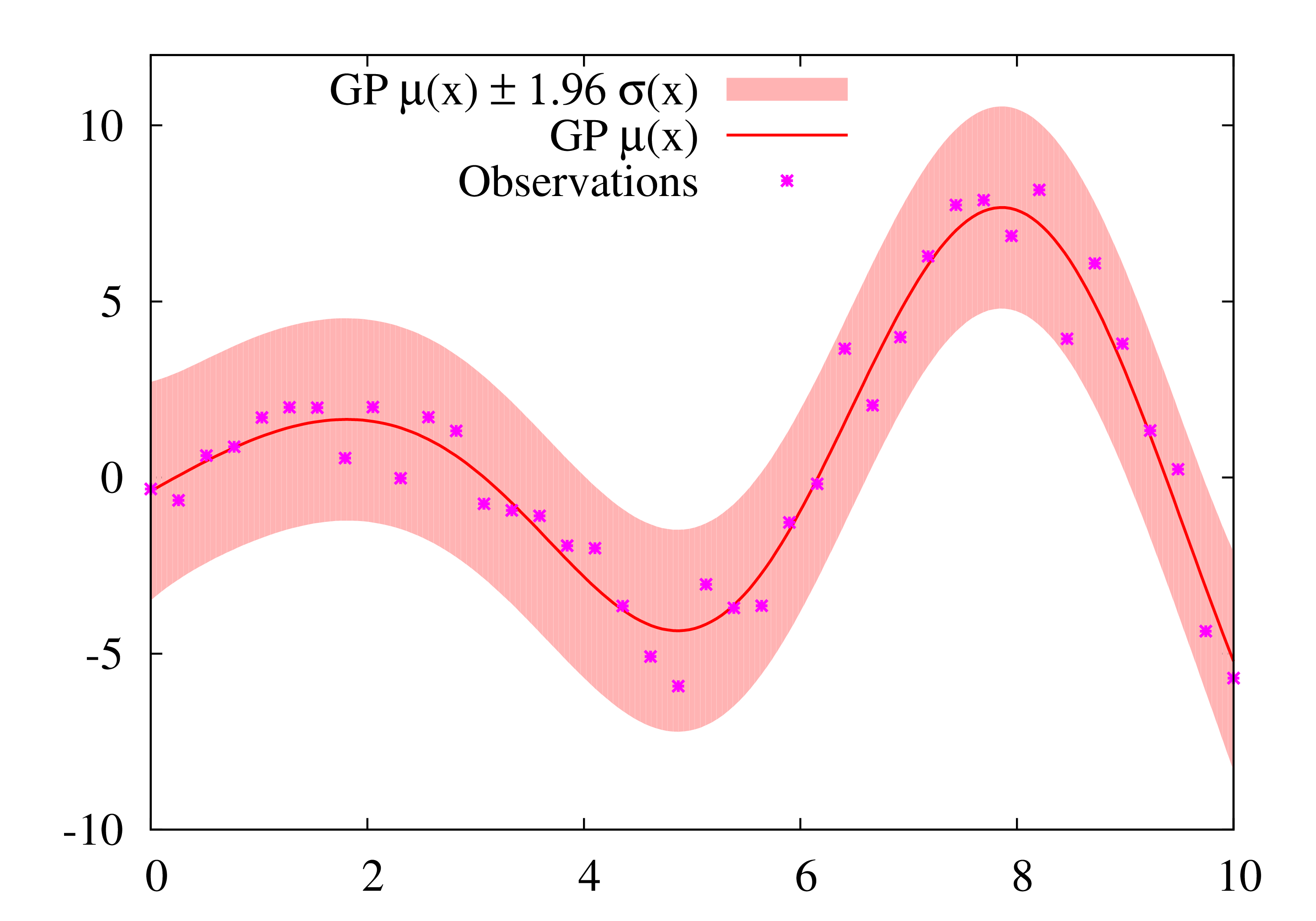
高斯过程回归
高斯过程回归（Gaussian Process Regression, GPR）是使用高斯过程（Gaussian Process, GP）先验对数据进行回归分析的非参数模型（non-parameteric model）。
GPR的模型假设包括噪声（回归残差）和高斯过程先验两部分，其求解按贝叶斯推断（Bayesian inference）进行。若不限制核函式的形式，GPR在理论上是紧緻空间（compact space）内任意连续函式的通用近似（universal approximator）。此外，GPR可提供预测结果的后验，且在似然为常态分配时，该后验具有解析形式。因此，GPR是一个具有泛用性和可解析性的机率模型。
基于高斯过程及其核函式所具有的便利性质，GPR在时间序列分析、图像处理和自动控制等领域的问题中有得到套用。GPR是计算开销较大的算法，通常被用于低维和小样本的回归问题，但也有适用于大样本和高维情形的扩展算法。
基本介绍
- 中文名：高斯过程回归
- 外文名：Gaussian Process Regression, GPR
- 类型：机器学习算法，非参数算法
- 提出者：Carl E. Rasmussen，Christopher K.I. Williams
- 提出时间：1996年
- 学科：统计学，人工智慧
- 套用：时间序列分析，图像处理，自动控制
历史
与GPR有关的早期研究大致可分为3部分，在时间序列分析中，安德雷·柯尔莫哥洛夫（Андрей Николаевич Колмогоров）和罗伯特·维纳（Robert Wiener）在二十世纪40年代提出了估计0均值平稳高斯过程信号的滤波技术。随后出现的卡尔曼滤波（Kalman filter）提供了估计高斯隐变数（latent variable）的有效方法。在地统计学领域，1963年提出的克里金法（Kriging）首次实现了平稳随机场的非参数回归，其后在二十世纪90年代出现的贝叶斯克里金提供了与GPR接近或等价的高斯随机场估计。在机器学习方面，包含无限节点的贝叶斯神经网路（Bayesian neural network）和各类核学习（kernel learning）方法例如核岭回归（kernel ridge regression）为GPR的核函式超参数求解带来了启发。
GPR作为机器学习一般方法的提出来自剑桥大学（University of Cambridge）学者Carl E. Rasmussen和爱丁堡大学（University of Edinburgh）学者Christopher K. I. Williams，二者在1996年发表的研究按函式空间观点给出了GPR的求解系统并讨论了GPR超参数的极大似然估计和蒙特卡罗方法求解。
理论
模型推导
这里给出GPR在权重空间（weight-space）观点和函式空间（function-space）观点下的模型推导，前者由贝叶斯线性回归（Bayesian linear regression）出发，通过特徵空间的映射得到GPR的预测形式，后者由高斯过程出发，以更简洁的方式得到与前者等价的结果。
权重空间观点
参见：贝叶斯线性回归
在权重空间（weight-space）观点下，GPR可以由正态假设的贝叶斯线性回归导出。具体地，给定相互独立的N组学习样本：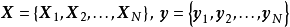
，贝叶斯线性回归是如下形式的多元线性回归模型：
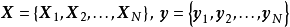
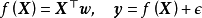
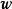
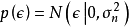
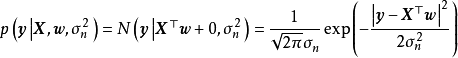
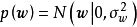
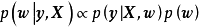
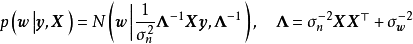
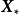
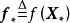
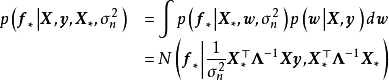
贝叶斯线性回归是一个线性参数模型，为使其表示样本间的非线性关係，可以使用给定的函式将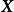
映射至高维空间：
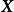
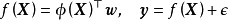
由于映射函式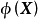
是固定的，即与模型权重无关，因此可直接带入贝叶斯线性回归的结果得到：
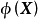
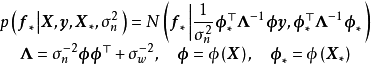
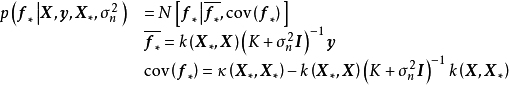
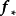
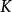
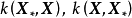
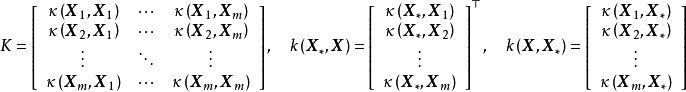
函式空间观点
参见：高斯过程
对回归模型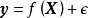
，若函式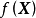
的形式不是固定的，则其为潜函式（latent function）。潜函式的每个取值都是函式空间（function-space）的一个测度。GPR取该函式空间的先验为高斯过程（Gaussian Process, GP），不失一般性，这里表示为0均值高斯过程：
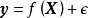
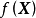
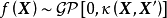
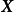
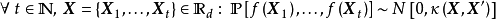
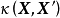
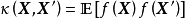
给定N组学习样本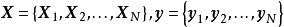
，作为对算法的推导，假设回归残差服从iid常态分配：
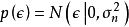，则GPR在高斯过程先验和常态分配似然下求解回归模型的后验：
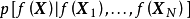，并对测试样本的测试结果进行估计（非正态似然的情形参见算法部分）。具体地，由回归模型和高斯过程的定义，
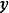和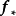
的机率分布为：
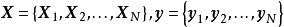
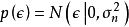
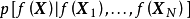
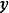
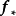
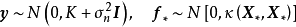
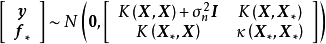
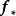
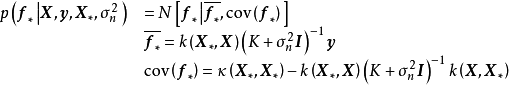
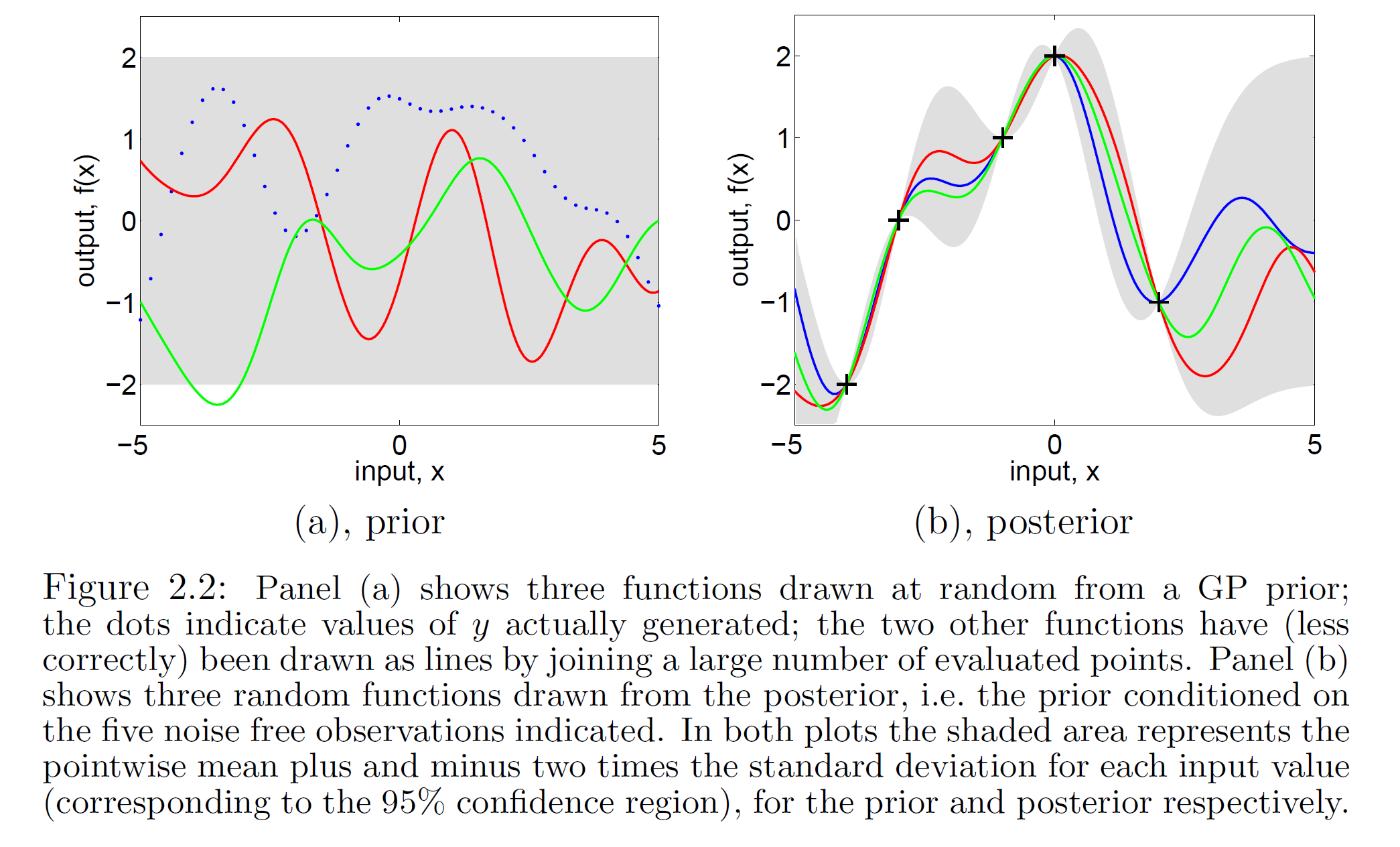一维高斯过程先验（左）和正态似然求解的后验（右）由上述预测形式的推导可知，GPR在假设0均值高斯过程先验时，解得的后验往往不是0均值的，因此0均值先验具有泛用性。但作为说明，GPR也可使用均值不为0的高斯过程先验，此时常见的做法是将潜函式表示为一组显式基函式（explicit basis function）：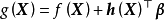
。在给定基函式的常态分配先验
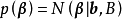时，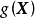
是具有如下形式的高斯过程：
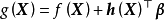
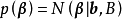
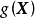
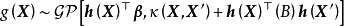
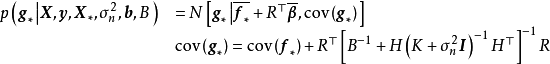
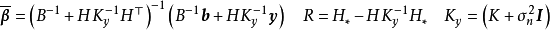
核函式
参见：核函式
GPR使用高斯过程作为先验，即假设了学习样本是高斯过程的採样，因此其估计结果与核函式有密切联繫。GPR中核函式的实际意义为协方差函式（covariance function），描述了学习样本间的相关性，因此其不是通过核方法简化计算的手段，而是模型假设的一部分。这里对GPR常见的核函式进行简单介绍，并引入核函式计算的加速方法。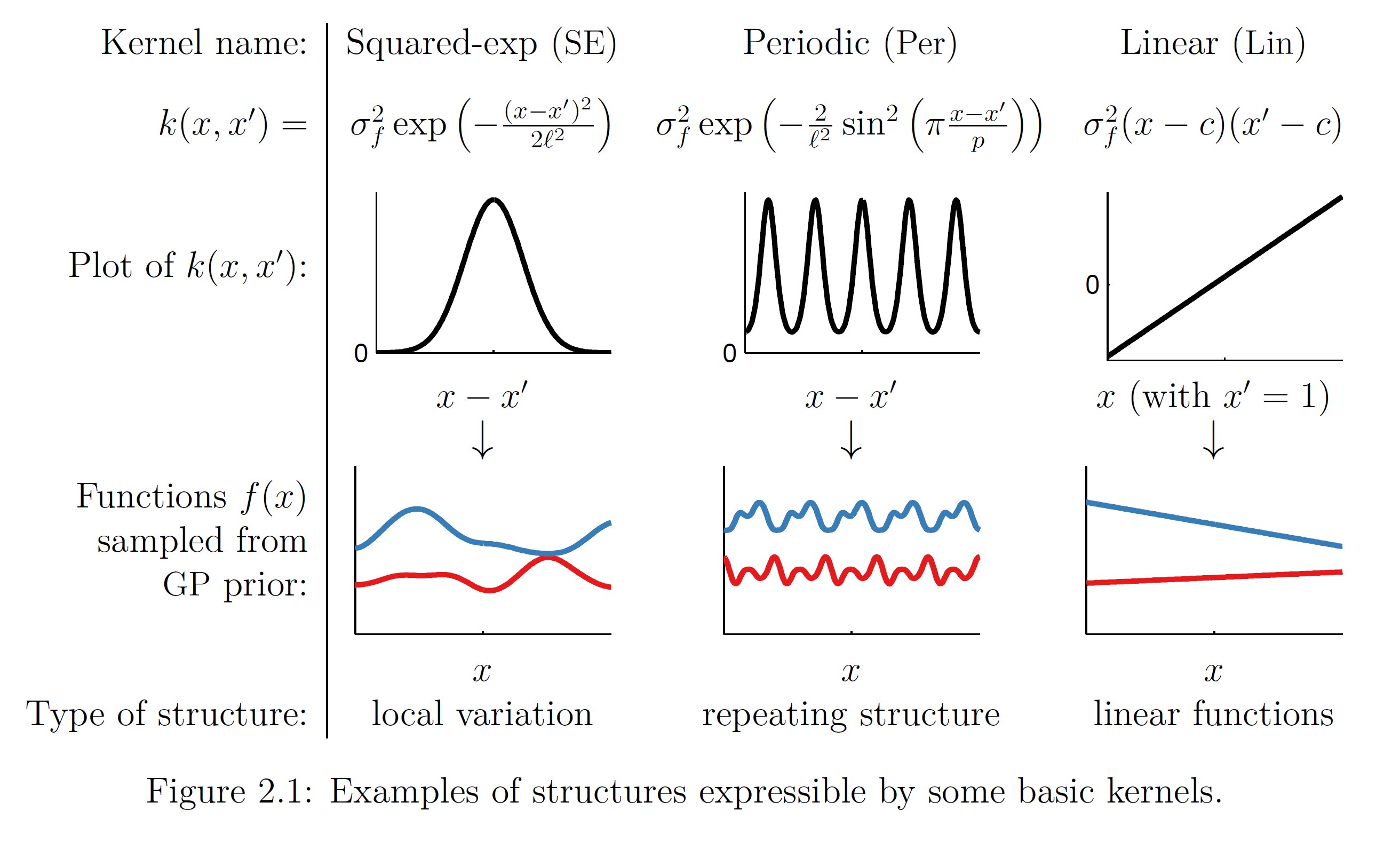
RBF核、周期核、线性核（上）和对应的高斯过程採样（下）
RBF核、周期核、线性核（上）和对应的高斯过程採样（下）核函式的选择
核函式的选择要求满足Mercer定理（Mercer's theorem），即核函式在样本空间内的任意格拉姆矩阵（核矩阵）为半正定矩阵（semi-positive definite）。
若GPR的先验为平移不变（transformation invariant）的平稳高斯过程时，可用的核函式包括径向基函式核（RBF kernel）、马顿核（Matérn kernel）、指数函式核（exponential kernel）、二次有理函式核（rational quadratic kernel, RQ kernel）等，以RBF核为例，其解析形式如下：
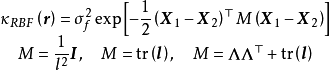
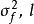
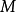
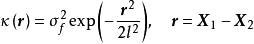
GPR也可使用非平稳高斯过程，此时常见的核函式选择为周期核（periodic kernel）与多项式函式核（polynominal kernel），二者分别赋予高斯过程周期性和旋转不变性（rotation invariant）。
核矩阵求逆的计算简化
由模型推导部分可知，GPR要求计算核矩阵的逆矩阵：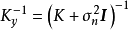
，若使用Cholesky分解（Cholesky decomposition）求逆，则对N组学习样本，其计算複杂度为
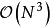。因此随着学习样本的增加，GPR的计算开销会显着增大。这里简单介绍核矩阵求逆的简化方法以应对上述问题，一般地，这些方法除GPR外也适用于其它核学习（kernel learning）方法，例如核岭回归、支持向量机（Support Vector Machine, SVM）等。
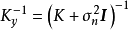
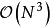
1. 选取数据子集（subset of datapoints, SD）
由于GPR可以在少量学习样本的情形下给出回归问题的可靠估计，因此从学习样本中合理选择一个子集可以显着降低核矩阵的大小，但不对GPR的表现造成显着影响。选取SD的常见方法是通过寻找微分熵（differential entropy）最大的学习样本作为支持向量定义SD，选取过程的计算複杂度为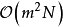
，在选取较小子集的情形下简化了计算，使用SD最佳化的高斯过程建模被称为稀疏高斯过程（sparse Gaussian process），或信息向量机（Informativevector machine, IVM）。
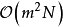
2. 低秩近似（low-rank approximation）
低秩近似将核矩阵近似为一系列低秩矩阵的乘积以简化求逆计算，具体地，N×N的核矩阵可以近似表示为：
，其中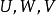
的大小分别为N×m、m×m、m×N，此时由Sherman-Morrison-Woodbury定理可得：
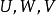
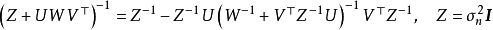
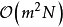
确定低秩矩阵的常见方法包括Nyström法（Nyström method）、子集回归法（subset ofregressors, SR）、映射过程近似（projected process approximation, PP）、BCM（Bayesian committee machine）等，这里对前两者进行介绍。Nyström法将核矩阵分解为4个分块矩阵并在构建低秩近似后直接带入GPR的预测形式：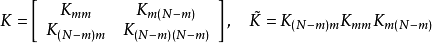
SR按与Nyström法相同的方式构建分块矩阵，但其首先将GPR的预测形式改写为核矩阵子集的回归併带入低秩矩阵，例如对GPR的均值部分有：
。
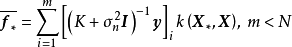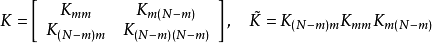
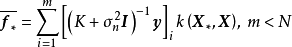
算法
正态似然
GPR的求解也被称为超参学习（hyper-parameter learning），是按贝叶斯方法通过学习样本确定核函式中超参数的过程。由贝叶斯定理（Bayes' theorem）可知，GPR的超参数后验有如下表示：
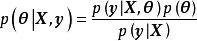
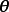
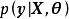
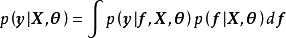
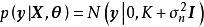
极大似然估计（Maximum Likelihood Estimation, MLE）
MLE通过令GPR的似然取极大值实现对超参数的单点估计。不失一般性，对0均值先验的GPR，带入联合常态分配的解析形式并求其负自然对数可得：
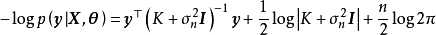
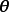
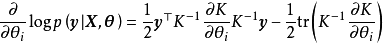
GPR的对数似然不是凸函式，且其最佳化複杂度随学习样本的增加而增大，在大量学习样本的情形下，可能会发现多个局部最优，且局部最优解的差异很大的情形，考虑解出的核函式超参数通常表示高斯过程的特徵长度尺度，多个局部最优意味着学习样本可以按多个尺度进行回归，其中小尺度的模型複杂度高但考虑更多局部特徵，大尺度的模型反之。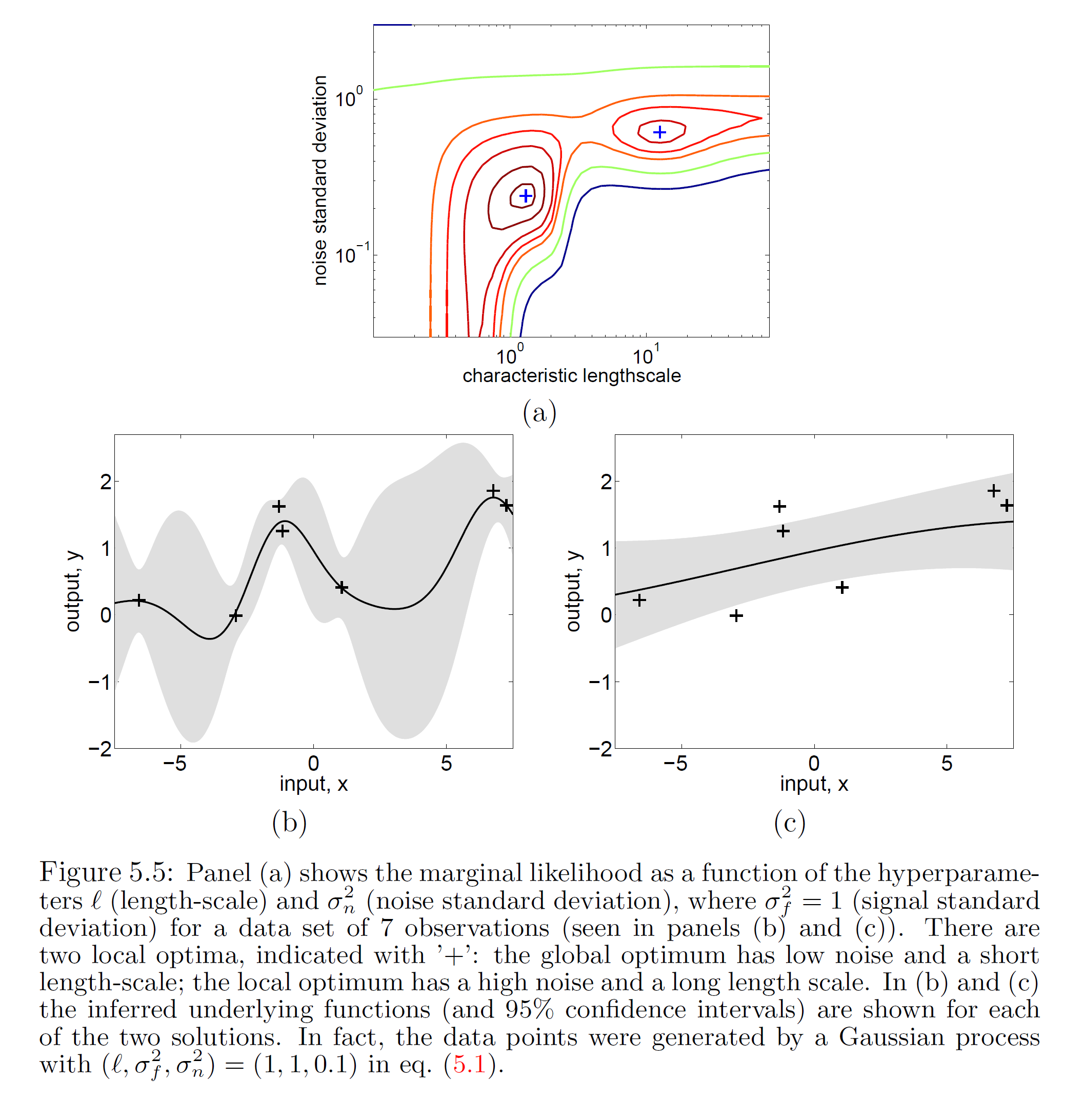
包含2个局部最优解的GPR对数似然（上）和得到的后验（下）
包含2个局部最优解的GPR对数似然（上）和得到的后验（下）除MLE外，GPR也可通过极大后验估计（Maximum A Posteriori estimation, MAP）求解。MAP是与MLE相近的估计方法，其最佳化目标是似然和先验的乘积。因为MAP与MLE在正态后验时得到的结果等价，在其他情形下的结果也相近，却引入了先验和额外的计算，因此在GPR研究中被较少提及。
极大伪似然估计（maximum pseudo-likelihood estimator, MPLE）
使用MPLE求解GPR的过程也被称为交叉验证（cross-validation），相比于MLE，其改变是对学习样本使用留一法（Leave One Out, LOO）计算其伪似然（pseudo-likelihood）的负自然对数：
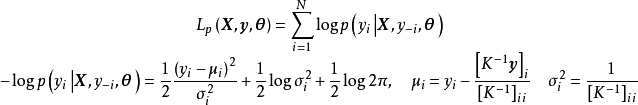
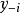
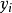
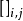
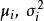
编程实现
这里提供一个使用GPy封装的GPR模型的例子：
# 导入模组import GPy # conda install -c conda-forge GPy import numpy as np# 生成学习样本N=100; sigma_n=0.2X = np.random.uniform(-2*np.pi, 2*np.pi,(N, 1))y = np.sin(X)+np.random.randn(N, 1)*sigma_n# 初始化RBF核: variance=1, lengthscale=1, variance of noise=0.1k_RBF = GPy.kern.RBF(1, 1, 0.1) # 建立GPR模型model = GPy.models.GPRegression(X, y, kernel=k_RBF)model.plot() # 绘製高斯过程先验model.optimize(messages=True) # 求解GPR超参数: MLE + 拟牛顿法（BFGS）model.plot(); # 绘製高斯过程后验# 单点预测mean, var = model.predict(np.array([[3*np.pi]]))print('Predicted mean and var at X=3pi: {}, {}'.format(mean, var))非正态似然
在似然不服从常态分配，例如处理异方差噪声数据时，GPR对测试数据的后验没有解析形式，此时可以使用的解析近似（analytical approximation）方法，例如拉普拉斯近似（Laplace Approximation, LA）和期望传播（Expectation Propagation, EP）将非正态后验近似表示为正态后验。LA和EP的推导可参见Rasmussen and Williams (2006), pp.41-60。
数值方法可用在非正态似然，或核函式超参数过多，不利于MLE问题最佳化的情形下求解GPR。选择包括蒙特卡罗方法（Monte Carlo）和变分贝叶斯估计（Variational Bayesian Inference, VBI）。VBI使用Jensen不等式得到GPR对数似然的凸函式下界作为代理损失并使用梯度算法求解，其优势是计算複杂度接近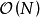
，显着简化了计算。蒙特卡罗方法被认为是在GPR数值解法中拥有高準确度和泛用性的方法，其原理是使用大量计算开销叠代生成随机数逼近GPR后验。蒙特卡罗求解GPR的常见方法为混合蒙特卡罗（Hybrid Monte Carlo, HMC），其步骤接近于Metropolis-Hastings算法，但通过“动量”项限制了随机游走的取值。HMC求解GPR的例子可参见Rasmussen (1996)。
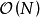
扩展算法
这里给出与高斯过程回归有关的扩展算法，但更一般地，这些方法是高斯过程模型的扩展，除回归问题外也可被套用于其它机器学习主题。
封装高斯过程（Warped Gaussian Process, WGP）
WGP通过对GPR进行非线性变换将其拓展至非高斯过程的情形，具体地，WGP首先在特徵空间选择一个单调封装函式（monotonic warping function），将学习样本变换至封装函式指定的潜空间后再求解包含封装函式超参数的极大似然。WGP的中封装函式的选择通常为双曲正切函式（hyperbolic tangent）线性组合，这里给出WGP对应于GPR的模型和算法：
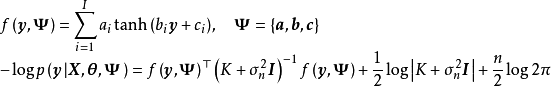
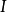
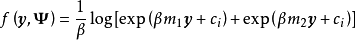
半参数高斯过程（Semi-parametric Gaussian Processes, SGP）
SGP是在回归问题中将高斯过程模型与参数模型线性组合以获得两者优点——GPR的灵活性和参数模型在高维问题中利用数据的有效性——的算法。具体地，SGPR构建了如下求解系统：
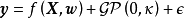
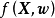
深度高斯过程（deep Gaussian Process, DGP）
由性质可知，高斯过程可以视为一个拥有单隐含层和无限个隐含层节点的多层感知器（Multi-Layer Perceptron, MLP），DGP是MLP由单隐含层推广至多隐含层时得到的高斯过程，即拥有多个隐含层和无限宽度的MLP。按定义，DGP是一组从高斯过程先验中选择的函式的分布：
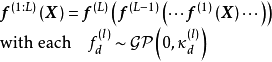
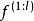
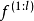
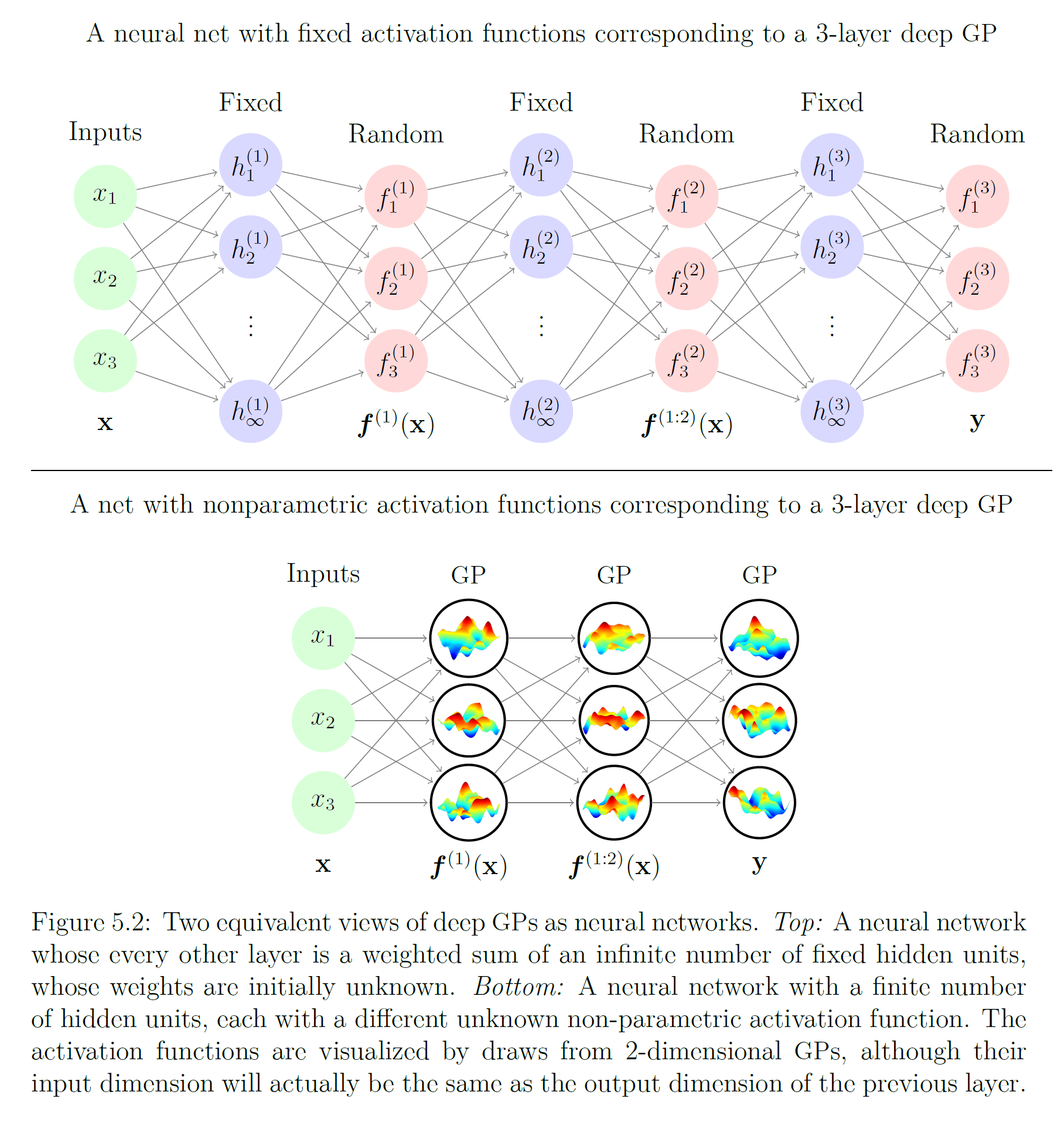由两种等价观点给出的DGP可加高斯过程（Additive Gaussian Process, AGP）
GPR的常见核函式，例如RBF核、马顿核等，被认为在高维特徵空间的学习问题中泛化能力较差，而AGP即是为解决GPR高维学习问题而提出的扩展方法。AGP利用核函式性质，在构建高斯过程先验时对核函式进行了组合和结构最佳化。介绍性地，AGP在不同维度将不同结构的核函式相加作为先验，并通过贝叶斯阶层核学习（Bayesian Hierarchical Kernel Learning, HKL）更新超参数以去除对学习样本解释不利的结构。以RBF核为例，其1阶可加高斯过程先验可表示为：
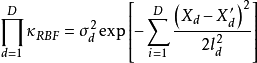
有关概念
高斯过程分类（Gaussian Process Classification, GPC）
GPC是使用高斯过程作为先验的分类器，在二元分类中，GPC在对潜函式进行估计后将其作为Sigmoid函式的输入得到分类机率；在多元分类中，则将Sigmoid函式替换为归一化指数函式。以二元分类为例，因为标籤数据是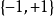
取值的二项分布随机变数，所以对应的GPC似然是潜函式对学习样本的因子乘积：
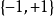
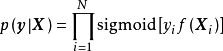
克里金法（Kriging）
主词条：克里金法
克里金法是与GPR相近的非参数模型，常见于随机场的插值问题。若协方差函式的形式等价，简单克里金（simple Kriging）和普通克里金（ordinary Kriging）的输出与GPR在正态似然下输出的数学期望相同，若克里金法使用高斯随机场假设，则给出的置信区间也与GPR相同。克里金法与GPR的不同点在于，前者假设随机场为固有平稳过程（intrinsically stationary process）并给出其对测试样本的最优无偏估计（Best Linear Unbiased Prediction, BLUP）；后者假设随机场为高斯过程并给出其对测试样本的完整后验。此外，考虑在地统计学中套用的常见情形，克里金法通常不加入噪声，其估计结果在学习样本处与学习目标完全相同。
有一些克里金法的扩展方法与GPR等价，例如Handcock and Stein (1993)和Handcock and Wallis (1994)提出的包含贝叶斯推断的克里金法使用了各向同性的马顿核高斯过程先验，并在正态似然假设下按MLE求解超参数。
性质
在使用特定核函式时，GPR是一个通用近似（universal approximator），具体地，若实数域内有紧緻空间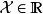
和赋范向量空间（normed vector space）
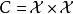，则可以证明，对任意函式
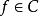，等价核（Equivalent Kernel, EK）构成的再生核希尔伯特空间（Reproducing Kernel Hilbert Space, RKHS）内总是存在
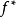能够按任意精度逼近原函式，即RKHS内总是存线上性组合：
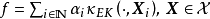。等价核的例子包括RBF核、二次有理函式核、指数函式核等。
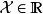
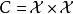
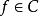
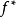
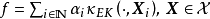
作为非参数高斯过程模型的性质：GPR的複杂程度取决于学习样本，因此天然避免了过拟合（overfitting）问题。当测试样本与学习样本在特徵空间的距离趋于无穷时，GPR的估计结果趋于其高斯过程先验，例如对0均值的各向同性高斯过程先验有：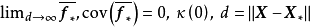
。由于高斯过程可以通过协方差函式模拟随机变数间的相关性，因此GPR可套用于平移不变、旋转不变或周期性数据的回归问题，但同时，由于核函式/非参数方法的局限，GPR在高维数据的学习中表现不佳，该现象有时被称为“维数诅咒（curse of dimensionality）”。此外由理论部分可知，GPR的计算複杂度较高。一些研究给出了计算量更低的改进算法并取得了效果，但总体而言，GPR是一个为小样本设计的机器学习算法。
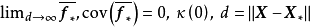
作为贝叶斯方法的性质：GPR是一个包含全贝叶斯特性（full Bayesian）的回归模型，可以给出测试数据的完整后验。此外，在似然为常态分配时，GPR给出的后验是具有闭合形式的联合常态分配，即GPR具有可解析性，该性质在非参数模型中并不多见。
与核学习方法的比较：GPR与适用于回归问题的核学习（kernel learning）方法，例如核岭回归、支持向量回归（support vector regression）等都使用了核函式与核方法，且可以通过相同的方式简化核矩阵求逆计算，但对后者，其核函式是输入空间向高维特徵空间的映射，而GPR中的核函式是高斯过程协方差函式的模型，表示随机变数间的相关性。上述不同在求解中的体现是，GPR的“学习”是通过数据确定核函式超参数的过程，而核方法的“学习”，是在给定核函式超参数后求解模型权重或寻找支持向量的过程。
与人工神经网路（Artificial Neural Network, ANN）的关係：ANN是参数模型，在理论和结构上与GPR有较大差异，但二者在套用中有重叠，例子包括时间序列分析和计算机视觉问题。若学习样本充足，ANN由于使用随机梯度下降方法进行学习，在求解效率上优势明显；但在要求给出机率输出时，GPR是更合适的方法。ANN中的多层感知器（Multi-Layer Perceptron, MLP）与高斯过程存在联繫，高斯过程可以由拥有单隐含层和无限个隐含层节点的MLP导出。具体地，对如下预测形式的MLP：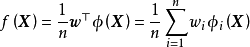
若其权重为iid随机变数且均值为0，方差为有限值，则由中心极限定理（central limit theorem）可推出，当隐含层节点数n趋于无穷时，模型输出的联合分布趋于0均值的联合常态分配：
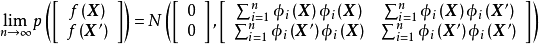该结论不要求iid权重服从常态分配，但当权重服从iid常态分配时，有限个隐含层节点的MLP也可表示为高斯过程。另一方面，MLP也可以由高斯过程导出，由Mercer定理可知，核函式可以表示为映射函式的内积：
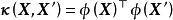，因此可视为以
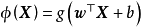为隐含层特徵（输出）的MLP。
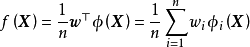
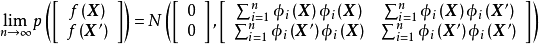
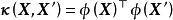
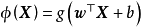
套用
GPR在各类低维的回归问题中均可套用，尤其是时间序列数据的预测，例子包括太阳辐射的有关变数、风速、土壤温度、冒纳罗亚观测站（Mauna Loa Observatory，MLO）的全球对流层平均二氧化碳浓度等。在图像处理（image processing）方面，GPR被用于图像去噪和生成超解析度图像。在自动控制方面，GPR被用于机械臂（robotic arm）数据的实时学习，也有研究开发了GPR的机器人学习（robot learning）系统。
包含GPR的编程模组
基于Python开发的机器学习模组scikit-learn提供封装的GPR工具GaussianProcessRegressor，其求解方法为BFGS算法（Broyden-Fletcher-Goldfarb-Shanno）的MLE，拥有自定义的求解器函式接口。在核函式方面，scikit-learn包含RBF核、马顿核、二次有理核、指数-周期核、多项式核以及自定义核函式的API工具。
由谢菲尔德机器学习团队（Sheffield machine learning group）开发的Python高斯过程建模工具GPy提供了GPR的完整求解系统和核函式，包括异方差噪声GPR、隐变数模型，解析近似、VBI和蒙特卡罗求解、稀疏高斯过程和低秩近似。此外有基于GPy的模型超参数最佳化工具GPyOpt可用。
pyGPs是基于Python开发的面向对象高斯过程建模套用，包含可视化学习界面，在功能上包括了常见核函式、稀疏高斯过程和解析近似。