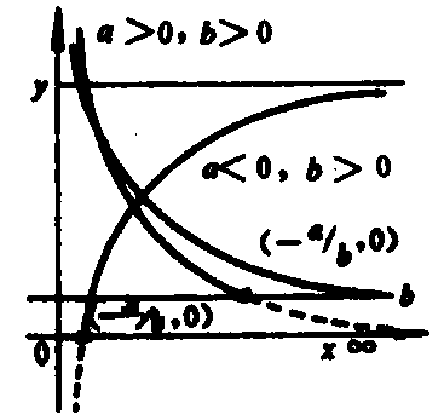
回归曲线
回归曲线,即曲线回归(curvilinear regression)或非线性回归(non-linear regression):两个变数间呈现曲线关係的回归,曲线回归是建立不同变数间相关关係的非线性数学模型数量关係式的统计方法。农业化学中各种因素间的相互关係多数是曲线关係。曲线回归分析或非线性回归分析:以最小二乘法分析曲线关係资料在数量变化上的特徵和规律的方法。
基本介绍
- 中文名:回归曲线
- 外文名:curvilinear regression(curve regression)
- 别名:曲线回归、非线性回归等
- 举例:多项式回归、正交多项式回归等
简介
曲线回归(curve regression) 是建立不同变数间相关关係的非线性数学模型数量关係式的统计方法,也称为非线性回归。农业化学中各种因素间的相互关係多数是曲线关係。
可化为直线的回归
可化为直线的回归是曲线回归中套用最广泛的形式。对某种形式的曲线回归模型取一定形式的变数变换,转换为线性回归模型,即可将曲线回归以线性回归的方法计算出式中各项参数,并进行统计检验和推断。可化为直线的曲线回归种类多样,常用的见表。
 图1 图1 | 公式: 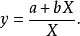 线性化方法: 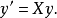 线性化后的线性方程: 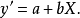 |
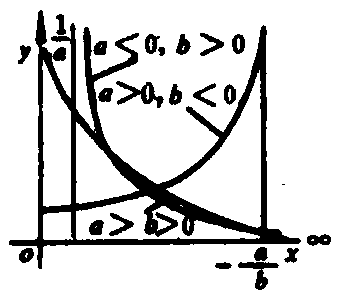 图2 图2 | 公式: 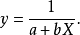 线性化方法: 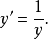 线性化后的线性方程: 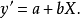 |
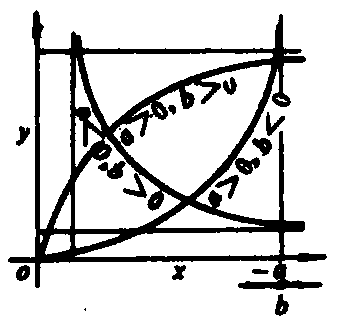 图 3 图 3 | 公式: 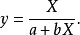 线性化方法: 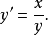 线性化后的线性方程: 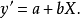 |
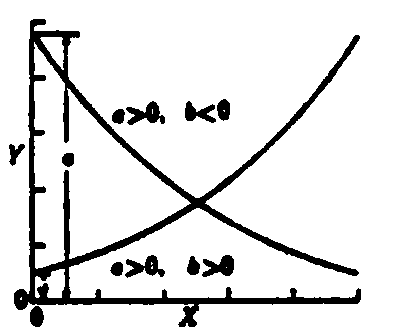 图4 图4 | 公式: 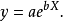 线性化方法: 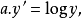 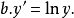 线性化后的线性方程: 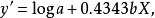 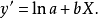 |
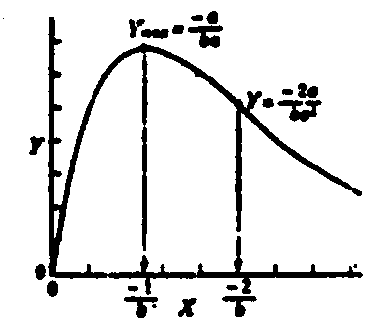 图5 图5 | 公式: 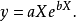 线性化方法: 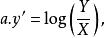 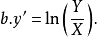 线性化后的线性方程: 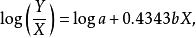 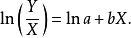 |
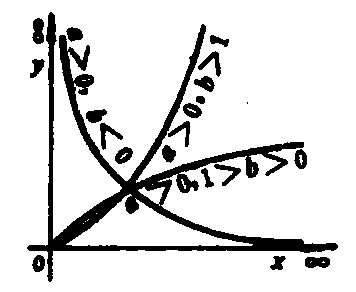 图5 图5 | 公式: 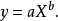 线性化方法: 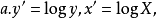 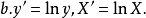 线性化后的线性方程: 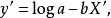 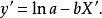 |
正交多项式回归
关于多项式回归,可参考相应词条。
多元线性回归及多项式回归的计算量随待估参数的数目增多而大量增加,而且各因素之间存在相关性。若需剔除不显着因素,则其他因素的回归係数需重新计算。解决这些困难的最常用办法是採用正交多项式,其前提是试验因素的水平间隔h要相等。对等间距水平的试验引进一族正交多项式,经数据变换后符合正交条件,从而消除了各因素之间相关性,并简化计算过程。正交多项式同样适用于多元多项式回归。
生长曲线
作物及养分吸收在生长初期较慢,达一定时间后积累迅速,以后又逐渐减缓,这种曲线大多呈S形,统称为生长曲线。这种理论曲线的模型呈正态曲线或近似于正态曲线。施肥对生长曲线的模型参数有明显影响,故在农业化学研究中亦常用生长曲线。生长曲线可分为从正态曲线假定出发及不以正态曲线出发两类。以正态假设出发的典型曲线是对称的S形曲线,其理论依据是将试验数据y转化为正态累积函式的标準差单位μ,当处理的水平变数为X时,则:
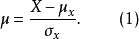
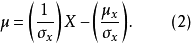
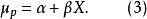
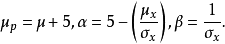
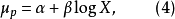
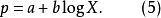

农化试验取得试验数据往往可用不同数学模型拟合,从中选定最适的模型可以缩小模型误差,这就需要从各种曲线回归模式中选择误差最小的一种,同时要注意儘可能在专业知识方面得到合理的解释。
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯