多元线性回归分析预测法
在市场的经济活动中,经常会遇到某一市场现象的发展和变化取决于几个影响因素的情况,也就是一个因变数和几个自变数有依存关係的情况。而且有时几个影响因素主次难以区分,或者有的因素虽属次要,但也不能略去其作用。例如,某一商品的销售量既与人口的增长变化有关,也与商品价格变化有关。这时採用一元回归分析预测法进行预测是难以奏效的,需要採用多元回归分析预测法。
多元回归分析预测法,是指通过对两个或两个以上的自变数与一个因变数的相关分析,建立预测模型进行预测的方法。当自变数与因变数之间存线上性关係时,称为多元线性回归分析。
基本介绍
- 中文名:多元线性回归分析预测法
- 外文名:Multi factor line regression method
- 别称:多元线性回归分析法
- 领域:统计学
多元线性回归的计算模型
一元线性回归是一个主要影响因素作为自变数来解释因变数的变化,在现实问题研究中,因变数的变化往往受几个重要因素的影响,此时就需要用两个或两个以上的影响因素作为自变数来解释因变数的变化,这就是多元回归亦称多重回归。当多个自变数与因变数之间是线性关係时,所进行的回归分析就是多元线性回归。
设y为因变数,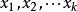 为自变数,并且自变数与因变数之间为线性关係时,则多元线性回归模型为:
为自变数,并且自变数与因变数之间为线性关係时,则多元线性回归模型为:
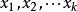
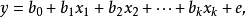
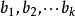
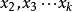
建立多元性回归模型时,为了保证回归模型具有优良的解释能力和预测效果,应首先注意自变数的选择,其準则是:
(1)自变数对因变数必须有显着的影响,并呈密切的线性相关;
(2)自变数与因变数之间的线性相关必须是真实的,而不是形式上的;
(3)自变数之间应具有一定的互斥性,即自变数之间的相关程度不应高于自变数与因变数之因的相关程度;
(4)自变数应具有完整的统计数据,其预测值容易确定。
多元性回归模型的参数估计,同一元线性回归方程一样,也是在要求误差平方和()为最小的前提下,用最小二乘法求解参数。以二线性回归模型为例,求解回归参数的标準方程组为:
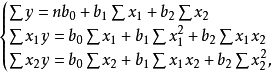
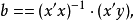
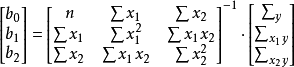
多元线性回归模型的检验
多元性回归模型与一元线性回归模型一样,在得到参数的最小二乘法的估计值之后,也需要进行必要的检验与评价,以决定模型是否可以套用。
1.拟合程度的测定。
与一元线性回归中可决係数r2相对应,多元线性回归中也有多重可决係数r2,它是在因变数的总变化中,由回归方程解释的变动(回归平方和)所占的比重,R2越大,回归方各对样本数据点拟合的程度越强,所有自变数与因变数的关係越密切。计算公式为:
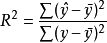
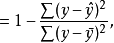
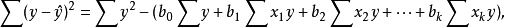
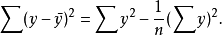
2.估计标準误差
估计标準误差,即因变数y的实际值与回归方程求出的估计值之间的标準误差,估计标準误差越小,回归方程拟合程度越程。
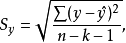
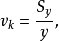
3.回归方程的显着性检验
回归方程的显着性检验,即检验整个回归方程的显着性,或者说评价所有自变数与因变数的线性关係是否密切。能常採用F检验,F统计量的计算公式为:
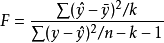
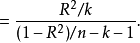
4.回归係数的显着性检验
在一元线性回归中,回归係数显着性检验(t检验)与回归方程的显着性检验(F检验)是等价的,但在多元线性回归中,这个等价不成立。t检验是分别检验回归模型中各个回归係数是否具有显着性,以便使模型中只保留那些对因变数有显着影响的因素。检验时先计算统计量ti;然后根据给定的显着水平a,自由度n-k-1查t分布表,得临界值ta或ta/ 2,t>t−a或ta/ 2,则回归係数bi与0有显着关异,反之,则与0无显着差异。统计量t的计算公式为:
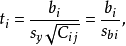
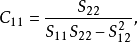
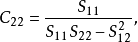
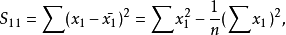
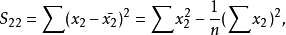
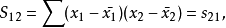
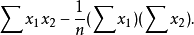
5.多重共线性判别
若某个回归係数的t检验通不过,可能是这个係数相对应的自变数对因变数的影平不显着所致,此时,应从回归模型中剔除这个自变数,重新建立更为简单的回归模型或更换自变数。也可能是自变数之间有共线性所致,此时应设法降低共线性的影响。
多重共线性是指在多元线性回归方程中,自变数之间有较强的线性关係,这种关係若超过了因变数与自变数的线性关係,则回归模型的稳定性受到破坏,回归係数估计不準确。需要指出的是,在多元回归模型中,多重共线性的难以避免的,只要多重共线性不太严重就行了。判别多元线性回归方程是否存在严惩的多重共线性,可分别计算每两个自变数之间的可决係数r,若r2>R2或接近于R2,则应设法降低多重线性的影响。亦可计算自变数间的相关係数矩阵的特徵值的条件数k= λ1/ λp(λ1为最大特徵值,λp为最小特徵值),k<100,则不存在多重点共线性;若100≤k≤1000,则自变数间存在较强的多重共线性,若k>1000,则自变数间存在严重的多重共线性。降低多重共线性的办法主要是转换自变数的取值,如变绝对数为相对数或平均数,或者更换其他的自变数。
6.D.W检验
当回归模型是根据动态数据建立的,则误差项e也是一个时间序列,若误差序列诸项之间相互独立,则误差序列各项之间没有相关关係,若误差序列之间存在密切的相关关係,则建立的回归模型就不能表述自变数与因变数之间的真实变动关係。D.W检验就是误差序列的自相关检验。检验的方法与一元线性回归相同。
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯