用连续曲线近似地刻画或比拟平面上离散点组所表示的坐标之间的函式关係的一种数据处理方法。用解析表达式逼近离散数据的一种方法。在科学实验或社会活动中，通过实验或观测得到量x与y的一组数据对(xi，yi)（i=1，2，…m），其中各xi是彼此不同的 。人们希望用一类与数据的背景材料规律相适应的解析表达式，y=f(x，c）来反映量x与y之间的依赖关係，即在一定意义下“最佳”地逼近或拟合已知数据。f(x，c)常称作拟合模型 ，式中c=(c1，c2，…cn)是一些待定参数。当c在f中线性出现时，称为线性模型，否则称为非线性模型。有许多衡量拟合优度的标準，最常用的一种做法是选择参数c使得拟合模型与实际观测值在各点的残差(或离差)ek=yk－f(xk，c)的加权平方和达到最小，此时所求曲线称作在加权最小二乘意义下对数据的拟合曲线。有许多求解拟合曲线的成功方法，对于线性模型一般通过建立和求解方程组来确定参数，从而求得拟合曲线。至于非线性模型，则要藉助求解非线性方程组或用最最佳化方法求得所需参数才能得到拟合曲线，有时称之为非线性最小二乘拟合。

曲线拟合

曲线拟合公式推导

曲线拟合：贝塞尔曲线与路径转化时的误差。值越大，误差越大；值越小，越精确。

曲线直线化是曲线拟合的重要手段之一。对于某些非线性的资料可以通过简单的变数变换使之直线化，这样就可以按最小二乘法原理求出变换后变数的直线方程，在实际工作中常利用此直线方程绘製资料的标準工作曲线，同时根据需要可将此直线方程还原为曲线方程，实现对资料的曲线拟合。

指数函式(exponential function)的标準式形式为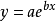

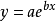
对上式两边取自然对数，得

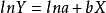
b>0时，Y随X增大而增大；b<0时，Y随X增大而减少。当以lnY和X绘製的散点图呈直线趋势时，可考虑採用指数函式来描述Y与X间的非线性关係，lna和b分别为截距和斜率。

更一般的指数函式

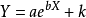
式中k为一常量，往往未知, 套用时可试用不同的值。

对数函式（lograrithmic function）的标準式形式为

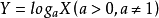
利用换底公式可得

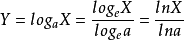
一般形式为

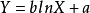
a>1时，Y随X增大而增大，先快后慢；0<a<1时，Y随X增大而减少，先快后慢。当以Y和lnX绘製的散点图呈直线趋势时，可考虑採用对数函式描述Y与X之间的非线性关係，式中的b和a分别为斜率和截距。

幂函式（power function）的标準式形式为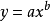

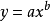
式中b>0时，Y随X增大而增大；b<0时，Y随X增大而减少。

对上式两边取对数，得

所以，当以lnY和lnX绘製的散点图呈直线趋势时，可考虑採用幂函式来描述Y和X间的非线性关係，lna和b分别是截距和斜率。

（一）绘製散点图，选择合适的曲线类型

一般根据资料性质结合专业知识便可确定资料的曲线类型，不能确定时，可在方格坐标纸上绘製散点图，根据散点的分布，选择接近的、合适的曲线类型。

曲线拟合

（二）进行变数变换

Y’=f(Y),X’=g(X)(12.37)

使变换后的两个变数呈直线关係。

（三）按最小二乘法原理求线性方程和方差分析

（四）将直线化方程转换为关于原变数X、Y的函式表达式