读书笔记摘抄新闻资讯
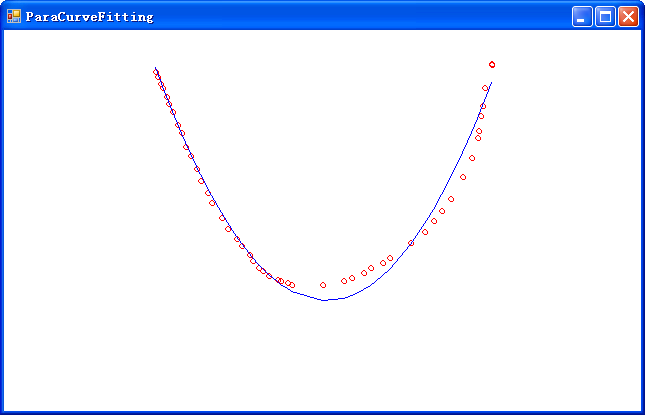
拟合
形象的说，拟合就是把平面上一系列的点，用一条光滑的曲线连线起来。因为这条曲线有无数种可能，从而有各种拟合方法。拟合的曲线一般可以用函式表示，根据这个函式的不同有不同的拟合名字。
常用的拟合方法有如最小二乘曲线拟合法等，在MATLAB中也可以用polyfit 来拟合多项式。拟合以及插值还有逼近是数值分析的三大基础工具，通俗意义上它们的区别在于：拟合是已知点列，从整体上靠近它们；插值是已知点列并且完全经过点列；逼近是已知曲线，或者点列，通过逼近使得构造的函式无限靠近它们。
基本介绍
- 中文名：拟合
- 外文名：fitting
- 学科：数理科学
- 类型：数学术语
- 定义：一条光滑的曲线把数据连线起来
- 方法：最小二乘曲线拟合法
拟合简介
如果待定函式是线性，就叫线性拟合或者线性回归(主要在统计中)，否则叫作非线性拟合或者非线性回归。表达式也可以是分段函式，这种情况下叫作样条拟合。
一组观测结果的数字统计与相应数值组的吻合。形象的说,拟合就是把平面上一系列的点，用一条光滑的曲线连线起来。因为这条曲线有无数种可能，从而有各种拟合方法。拟合的曲线一般可以用函式表示，根据这个函式的不同有不同的拟合名字。
在MATLAB中可以用polyfit 来拟合多项式。
拟合以及插值还有逼近是数值分析的三大基础工具，通俗意义上它们的区别在于：拟合是已知点列，从整体上靠近它们；插值是已知点列并且完全经过点列；逼近是已知曲线，或者点列，通过逼近使得构造的函式无限靠近它们。
拟合优度
R^2衡量的是回归方程整体的拟合度，是表达因变数与所有自变数之间的总体关係。R^2等于回归平方和在总平方和中所占的比率，即回归方程所能解释的因变数变异性的百分比。实际值与平均值的总误差中，回归误差与剩余误差是此消彼长的关係。因而回归误差从正面测定线性模型的拟合优度，剩余误差则从反面来判定线性模型的拟合优度。
统计上定义剩余误差除以自由度n – 2所得之商的平方根为估计标準误。为回归模型拟合优度的判断和评价指标，估计标準误显然不如判定係数R^2。R^2是无量纲係数，有确定的取值範围(0—1)，便于对不同资料回归模型拟合优度进行比较；而估计标準误差是有计量单位的，又没有确定的取值範围，不便于对不同资料回归模型拟合优度进行比较。
金融的套用和解释：
拟合优度是一个统计术语，是衡量金融模型的预期值和现实所得的实际值的差距。
它是一种统计方法套用于金融等领域，基于所得观测值的基础上作出的预测。换句话说，它是衡量如何将实际观测的数值进行模拟的相关预测。
曲线拟合
实际工作中，变数间未必都有线性关係，如服药后血药浓度与时间的关係；疾病疗效与疗程长短的关係；毒物剂量与致死率的关係等常呈曲线关係。曲线拟合（curve fitting）是指选择适当的曲线类型来拟合观测数据，并用拟合的曲线方程分析两变数间的关係。
最小二乘法（又称最小平方法）是一种数学最佳化技术。它通过最小化误差的平方和寻找数据的最佳函式匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些最佳化问题也可通过最小化能量或最大化熵用最小二乘法来表达。
给定一组测量数据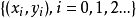
，基于最小二乘原理，求得变数x和y之间的函式关係f(x,A)，使它最佳地逼近或拟合已知数据。f(x,A)称为拟合模型，
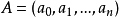是一些待定参数。做法是选择参数A使得拟合模型与实际观测值在各点的残差
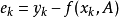的加权平方和最小。套用此法拟合的曲线称为最小二乘拟合曲线。
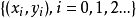
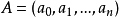
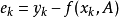
用最小二乘法求拟合曲线首先要确定拟合模型f(x)，一般来说，根据各门科的知识可以大致确定函式的所属类，若不具备这些知识，则通常从问题的运动规律及给定数据的散点图来确定拟合曲线的形式。
拟合工具
MATLAB曲线拟合工具箱
简介
MATLAB做曲线拟合可以通过内建函式或者曲线拟合工具箱(Curve Fitting Toolbox)。这个工具箱集成了用MATLAB建立的图形用户界面(GUIs)和M档案函式。利用这个工具箱可以进行参数拟合(当想找出回归係数以及他们背后的物理意义的时候就可以採用参数拟合)，或者通过採用平滑样条或者其他各种插值方法进行非参数拟合(当回归係数不具有物理意义并且不在意他们的时候，就採用非参数拟合方法)。利用这个界面，可以快速地在简单易用的环境中实现许多基本的曲线拟合。
改善拟合结果
很多因素会对曲线拟合产生影响，导致拟合效果又好有坏，这里仅从一些角度出发探讨有可能改善拟合质量。
1）模型的选择:这是最主要的一个因素，试着用各种不同的模型对数据进行拟合比较;
2）数据预处理:在拟合前对数据进行预处理也很有用，这包括对回响数据进行变换以及剔除Infs、NaNs，以及有明显错误的点。
3）合理的拟合应该具有处理出现奇异而使得预测趋于无穷大的时候的能力。
4）知道越多的係数的估计信息，拟合越容易收敛。
5）将数据分解为几个子集，对不同的子集採用不同的曲线拟合。
6）複杂的问题最好通过进化的方式解决，即一个间题的少量独立变数先解决。低阶问题的解通常通过近似映射作为高阶问题解的起始点。