浮点精细度
浮点简单讲就是实数的意思,浮点数在计算机中用以近似表示任意某个实数。具体的说,这个实数由一个整数或定点数(即尾数)乘以某个基数(计算机中通常是2)的整数次幂得到,这种表示方法类似于基数为10的科学记数法。浮点精细度就是实数的精细程度。
基本介绍
- 中文名:浮点精细度
- 外文名:Floating point precision
- 套用领域:计算机
- 本质:实数的精细程度
- 换算方式:二进制
- 学科:数理科学
浮点数字
一个数字表示指定编码数字,通常为一个数字串的某种方式。
有几种数字字元串可以代表数字的机制。在通用数学符号中,数字串可以是任意长度的,并且小数点的位置通过在那里放置明确的“点”字元(点或逗号)来指示。如果没有指定小数点,那幺字元串隐含地表示一个整数,并且未指定的小数点将离开字元串的右端,在最低有效数字的旁边。在定点系统中,字元串中的位置是为小数点指定的。所以一个定点方案可能是使用一个小数点位于中间的8位十进制数字串,其中“00012345”代表0001.2345。
在科学记数法中,给定的数字是以10的幂来缩放的,以便它位于一定的範围内,通常在1到10之间,小数点紧跟在第一个数字之后。比例因子作为十的幂,然后在数字的末尾单独指示。例如,木星的月亮Io的轨道周期为152,853.5047秒,这个值将以标準形式的科学记数法表示为1.528535047×10秒。
浮点表示在概念上与科学记数法类似。从逻辑上讲,浮点数包括:
- 给定基数(或基数)中给定长度的带符号(意义是负数或非负数)字元串。这个数字串被称为有效数,尾数或係数。有效数字的长度决定了数字可以表示的精度。假定小数点位置始终位于有效位数内的某个位置 - 通常在最高有效位之后或最前面的数字之前,或者在最右边(最不重要)位的右侧。这篇文章一般遵循约定,小数点被设定在最重要的(最左边的)数字之后。
- 有符号的整数指数(也称为特徵或比例),用于修改数字的大小。
为了导出浮点数的值时,有效数由乘以基升高到的功率指数,相当于由等于的指数对值的号码的地方移位从它隐含位置小数点如果指数是正值,则表示右边,如果指数是负值,则表示为左边。
以base-10(熟悉的十进制符号)为例,编号为152,853.5047的精度为十位十进制数字,表示为有效数字1,528,535,047以及5作为指数。为了确定实际值,在有效数字的第一位之后放置一个小数点,结果乘以10得到1.528535047×10或152,853.5047。在存储这样一个数字时,基础(10)不需要被存储,因为它对于整个支持的数字範围是相同的,因此可以推断出来。
象徵性地,这个最终值是:

其中s是有效数字(忽略任何隐含的小数点),p是精度(有效数字中的位数),b是基数(在我们的例子中,这是数字10),e是指数。
在历史上,已经使用了几个数字基数来表示浮点数,其中基数二(二进制)是最常见的,其次是十进制(十进制),以及其他不太常见的变体,例如十六进制(十六进制)甚至基地三(见Setun)。
浮点数是一个有理数,因为它可以表示为一个整数除以另一个;例如1.45×10是(145/100)×1000或145,000/ 100。基数决定了可以表示的分数;例如,1/5不能完全表示为使用二进制基数的浮点数,但1/5可以精确地用小数(0.2或2×10)表示。然而,1/3不能用二进制(0.010101 ...)或十进制(0.333 ...)来表示,但是在基数3中,它是微不足道的(0.1或1×3)。发生无限扩展的场合取决于基础及其主要因素,如位置标记文章中所述。
有效数(包括其符号)和指数存储在计算机中的方式取决于实现。常见的IEEE格式在后面和其他地方详细描述,但作为例子,在二进制单精度(32位)浮点表示中,{\ displaystyle p = 24},所以有效位是一个24位的字元串。例如,数字π的前33位是:

在这个二进制扩展中,让我们表示从0(最左边的位或最高有效位)到32(最右边的位)的位置。24位有效位将在位置23停止,如上面带下划线的位0所示。下一位,在位置24,被称为圆位或舍位位。它用于将33位近似值四捨五入为最接近的24位数(对于中途值有特定的规则,这里不是这种情况)。在这个例子中,该位是1,被加到由最左边的24位形成的整数上,产生:
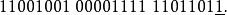
当这是使用IEEE 754编码存储在存储器中,这成为有效数小号。假定有效位在最左边的位右边有一个二进制点。
可以要求非零数字的有效位的最高有效位数不为零(除非相应的指数小于最小数字)。这个过程被称为规範化。对于二进制格式(仅使用数字0和1),此非零数字必须为1。因此,它不需要在记忆体中表示;允许格式有更多的精度。这个规则被不同地称为前导位约定,隐式位约定或隐藏位约定。
浮点数範围
浮点数由两个定点组件组成,其範围完全取决于表示中的位数或位数。虽然分量线性取决于它们的範围,但是浮点範围线性地依赖于指数分量範围内的显着範围和指数函式,这在数量上显着地增大了範围。
在典型的计算机系统中,“双精度”(64位)二进制浮点数的係数为53位(其中一个隐含),指数为11位,符号位为1。由于指数的範围是[-1022,1023],而308大约是log10(2),所以此格式的正浮点数的範围大约在10到10。格式的完整範围从大约-10到+10(见IEEE 754)。
系统(B,P,L,U)中的归一化浮点数的数量
- B是系统的基础,
- P是系统对P数的精度,
- L是系统中可表示的最小指数,
- 和ü是在系统中使用的最大的指数)
是 

有一个最小的正归一化浮点数,下溢级别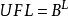 其中以1为前导数字,0为有效数字的剩余数字,以及指数的最小可能值。
其中以1为前导数字,0为有效数字的剩余数字,以及指数的最小可能值。
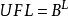
有一个最大的浮点数,溢出级别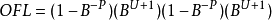 其中B-1是有效数字的每个数字的值,并且是指数的最大可能值。
其中B-1是有效数字的每个数字的值,并且是指数的最大可能值。
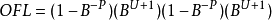
另外,在-UFL和UFL之间还有可表示的值。即,正数和负数的零,以及非规格化的数字。
IEEE 754:现代计算机中的浮点
| 浮点精度 |
|---|
|
|
|
在IEEE标準化二进制浮点数字的计算机表示在IEEE 754在1985年(又名IEC 60559)这个第一标準之后,几乎所有现代机器。2008年进行了修订。IBM大型机除支持IEEE 754二进制格式外,还支持IBM自己的十六进制浮点格式和IEEE 754-2008十进制浮点数。在克雷T90系列有一个IEEE版本,但SV1仍然使用的Cray浮点格式。
该标準提供了许多密切相关的格式,只有少数细节不同。其中五种称为基本格式,另一种称为扩展格式;其中三个特别广泛地用于计算机硬体和语言:
- 单精度,通常用于表示C语言系列中的“float”类型(虽然这不能保证)。这是一个二进制格式,占用32位(4位元组),其有效位数的精度为24位(约7位十进制数字)。
- 双精度,通常用来表示C语言系列中的“double”类型(虽然不能保证)。这是一个占用64位(8位元组)的二进制格式,其有效位数的精度为53位(约16位十进制数字)。
- 双扩展,也称为“扩展精度”格式。这是一个二进制格式,占用至少79位(如果不使用隐藏/隐式位规则,则为80位),其有效位数的精度至少为64位(19位十进制数)。x86体系结构提供了满足最低要求(64位精度,15位指数,从而适应80位)的格式。通常在这样的处理器上,这种格式可以在C语言系列(C99和C11)中使用“long double”标準“IEC 60559浮点运算扩展 - 附属档案F”推荐将80位扩展格式提供为“长双”(如果可用))。在其他处理器上,如果任何形式的扩展精度不可用,“long double”可能是“double”的同义词,或者可能代表更大的格式,如四倍精度。
增加浮点表示的精度通常会减少由中间计算引起的累积捨入误差量。不太常见的IEEE格式包括:
- 四倍精度(binary128)。这是一个占用128位(16位元组)的二进制格式,其有效位数的精度为113位(约34位)。
- 双精度(decimal64)和四精度(decimal128)十进制浮点格式。这些格式与单精度(decimal32)格式一起,用于正确执行小数四捨五入。
- 一半,也称为binary16,一个16位浮点值。它正在使用NVIDIACg图形语言和openEXR标準。
任何绝对值小于2整数都可以用单精度格式精确表示,绝对值小于2任何整数都可以用双精度格式精确表示。而且,可以表示这样一个数字的2倍的广泛的权力。这些属性有时用于纯粹的整数数据,在具有双精度浮点数但只有32位整数的平台上得到53位整数。
该标準指定了一些特殊的值,它们的表示形式:正无穷(+∞),负无穷(-∞),与普通(“正”)零不同的负零(-0)和“不是数值”NaNs)。
按照IEEE标準定义的浮点数比较与通常的整数比较有点不同。负的和正的零比较相等,每个NaN比较不等于每个值,包括它本身。除了NaN,所有的值都严格小于+∞,严格大于-∞。有限的浮点数以与它们的值相同的方式排列(在实数集合中)。
内部表示
浮点数通常从左到右被打包成一个计算机数据,作为符号位,指数栏位和有效数或尾数。对于具有现存硬体实现的IEEE 754二进制格式(基本和扩展),它们分配如下:
| 类型 | 标誌 | 指数 | 重要的领域 | 总比特数 | 指数偏差 | 比特精度 | 小数位数 |
|---|---|---|---|---|---|---|---|
一半(IEEE 754-2008) | 1 | 五 | 10 | 16 | 15 | 11 | 〜3.3 |
单 | 1 | 8 | 23 | 32 | 127 | 24 | 〜7.2 |
双 | 1 | 11 | 52 | 64 | 1023 | 53 | 〜15.9 |
x86扩展精度 | 1 | 15 | 64 | 80 | 16383 | 64 | 〜19.2 |
四 | 1 | 15 | 112 | 128 | 16383 | 113 | 〜34.0 |
指数可以是正数,也可以是负数,二进制格式的数据存储为一个无符号数字,加上一个固定的“偏差”。该栏位中所有0的值保留为零和低于正常的数字;全1的值保留给无穷大和NaN。归一化数字的指数範围为[-126,127]为单精度,[-1022,1023]为双精度,或[-16382,16383]为四。规範化的数字不包括低于正常值,零,无穷和NaN。
在IEEE二进制交换格式中,标準化的有效位的前1位实际上并不存储在计算机数据中。它被称为“隐藏”或“隐含”位。正因为如此,单精度格式实际上有24位精度的有效位数,双精度格式有53位,四位有113位精度。
例如,上面显示的是π,四捨五入到24位的精度,具有:
- sign = 0;e= 1;s= 110010010000111111011011(含隐藏位)
指数偏差(127)和指数(1)的总和为128,所以这是以单精度格式表示为
- 0 10000000 10010010000111111011011(不含隐藏位)= 40490FDB为十六进制数。
分段线性逼近指数和对数
如果我们绘製一个点阵图模式的浮点值(x轴是位模式,被认为是整数,y轴是浮点数的值;假设是正的),可以得到移位的分段线性近似值基数为2的缩放指数函式, (因此实际上
(因此实际上  )。相反,给定一个实数,如果採用浮点表示法并将其视为一个整数,则可以得到移位和缩放的基2对数的分段线性近似,
)。相反,给定一个实数,如果採用浮点表示法并将其视为一个整数,则可以得到移位和缩放的基2对数的分段线性近似, (因此实际上
(因此实际上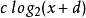 ),如右图所示。
),如右图所示。



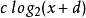
这种解释对于显示浮点数的值随着表示的变化是有用的,并且允许通过整数运算和位移对浮点运算进行某些有效的近似。例如,将float重新解释为一个整数,取其负数(或者从一个固定的数字中减去,由于偏差和隐含的1),然后重新解释为一个浮点数,得到倒数。明显地,忽略有效数,取倒数只是取(无偏)指数的加法倒数,因为倒数的指数是原指数的负数。(因此,实际上从偏差的两倍中减去指数,这对应于非偏置,取负,然后偏置。)对于有效数,近似1倒数近似为线性: (因为衍生物是
(因为衍生物是  ;这是泰勒级数的第一项),因此对于有效数据,取负数(或者从固定数减去处理隐含1)近似取倒数。
;这是泰勒级数的第一项),因此对于有效数据,取负数(或者从固定数减去处理隐含1)近似取倒数。


更重要的是,位移允许计算平方(左移1)或取平方根(右移1)。这导致近似计算平方根;结合之前的逆向技术,这允许在20世纪80年代末和90年代在图形处理中重要的快速平方根计算。这可以在其他一些套用中被利用,例如数字声音处理中的音量增加。
具体地说,每次指数递增时,数值加倍(因此按指数增长),而每次有效数递增(对于给定的指数),数值增加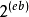 (因此线性增长,斜率等于指数的实际值(无偏))。即使对于给定指数的最后一步,其中有效数溢出到指数中:对于隐含1,1.11 ... 1之后的数是2.0(不管指数),即指数的增量:
(因此线性增长,斜率等于指数的实际值(无偏))。即使对于给定指数的最后一步,其中有效数溢出到指数中:对于隐含1,1.11 ... 1之后的数是2.0(不管指数),即指数的增量:
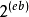
- (0 ... 001)0 ... 0到(0 ... 001)1 ... 1,(0 ... 010)0 ... 0是相同的步长(线性)
因此,作为一个图形,它是线性的(对于一个给定的指数,随着有效数字的增长)连线两个均匀间隔的幂(当有效数为0时),每个线性片具有前一个斜率的两倍:它大约是一个缩放并转移指数 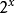 。每件作品採用相同的水平空间,但最后的两倍是垂直空间。由于指数是凸起的,因此通过有效数为0的点,该值总是大于或等于实际(移位和缩放的)指数曲线;通过略有不同的转变,人们可以更接近于指数,有时高估,有时低估。相反,将一个浮点数解释为一个整数给出了一个近似的移位和缩放对数,每个块都有最后一个斜率的一半,取相同的垂直空间,但水平空间的两倍。由于对数是向下凸的,所以近似值总是较小比对应的对数曲线;再次,一个不同的尺度和偏移选择(如右上方)产生了一个更接近的近似值。
。每件作品採用相同的水平空间,但最后的两倍是垂直空间。由于指数是凸起的,因此通过有效数为0的点,该值总是大于或等于实际(移位和缩放的)指数曲线;通过略有不同的转变,人们可以更接近于指数,有时高估,有时低估。相反,将一个浮点数解释为一个整数给出了一个近似的移位和缩放对数,每个块都有最后一个斜率的一半,取相同的垂直空间,但水平空间的两倍。由于对数是向下凸的,所以近似值总是较小比对应的对数曲线;再次,一个不同的尺度和偏移选择(如右上方)产生了一个更接近的近似值。
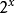
机器精度和后向误差分析
机器精度是表征浮点系统精度的量,用于浮点算法的后向错误分析。它也被称为单位捨入或机器epsilon。通常表示为Emach,其值取决于所使用的特定捨入。
四捨五入为零,
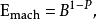
而捨入到最近,
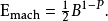
这很重要,因为它限制了在浮点系统的标準化範围内表示任何非零实数x的相对误差:
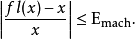
向后的误差分析,其理论由James H. Wilkinson开发和推广,可以用来确定实现数值函式的算法在数值上是稳定的。基本的方法是表明虽然计算结果由于捨入误差而不会是完全正确的,但对于附近有轻微干扰的输入数据的问题来说,这是确切的解决方案。如果所需的扰动很小,则按照输入数据中的不确定性的顺序,那幺结果在某种意义上与数据“应得”一样準确。算法被定义为后向稳定。稳定性是对给定数值过程的捨入误差敏感度的度量;相比之下,条件编号对于一个给定的问题的函式表示该函式对其输入中的小扰动的内在敏感性,并且与用于解决该问题的实现无关。
作为一个简单的例子,考虑一个简单的表达式给出(长度二)向量的内积  和
和  , 然后
, 然后



其中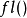 指示正确捨入的浮点运算
指示正确捨入的浮点运算
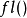
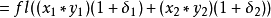
其中 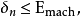 , 从上面
, 从上面
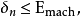


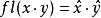
其中


其中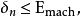
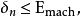
这是两个微扰(Emach的数量级)输入数据的总和,所以是后向稳定的。数值线性代数中更实际的例子见Higham 2002和下面的其他参考文献。
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯