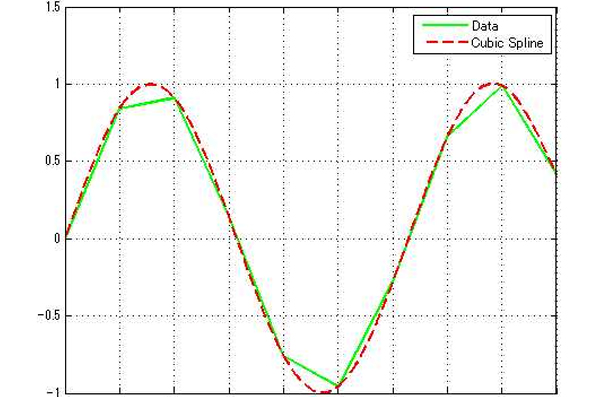
三次样条插值
三次样条插值(Cubic Spline Interpolation)简称Spline插值,是通过一系列形值点的一条光滑曲线,数学上通过求解三弯矩方程组得出曲线函式组的过程。
实际计算时还需要引入边界条件才能完成计算。一般的计算方法书上都没有说明非扭结边界的定义,但数值计算软体如Matlab都把非扭结边界条件作为默认的边界条件。
基本介绍
- 中文名:三次样条插值
- 外文名:Cubic Spline Interpolation
- 简称:Spline插值
- 性质:数学术语
- 基础:样条插值
- 套用:数学工程等
基本概念
早期工程师製图时,把富有弹性的细长木条(所谓样条)用压铁固定在样点上,在其他地方让它自由弯曲,然后沿木条画下曲线。成为样条曲线。
相关函式
三次样条函式:
定义:函式S(x)∈C2[a,b] ,且在每个小区间[ xj,xj+1 ]上是三次多项式,其中
a =x0 <x1<...< xn= b 是给定节点,则称S(x)是节点x0,x1,...xn上的三次样条函式。
若在节点x j 上给定函式值Yj= f (Xj).( j =0, 1, , n) ,并成立
S(xj ) =yj .( j= 0, 1, , n) ,则称S(x)为三次样条插值函式。
实际计算时还需要引入边界条件才能完成计算。边界通常有自然边界(边界点的二阶导为0),夹持边界(边界点导数给定),非扭结边界(使两端点的三阶导与这两端点的邻近点的三阶导相等)。一般的计算方法书上都没有说明非扭结边界的定义,但数值计算软体如Matlab都把非扭结边界条件作为默认的边界条件。
数学表达式
一种常用的样条插值设[a,b]上的插值节点构成[a,b]的一个分划Δ:a=x0<x1<…<xn=b,f(x)于各节点的值是f(xi)=fi(i=0,1,…,n).三次样条插值问题是求[a,b]上关于分划Δ的三次样条函式s(x).根据s(x)应满足的两个条件于[xi,xi+1],有
其中hi=xi+1-xi (i=0,1,…,n-1),Mi=s″(xi)为待定参数.M0,M1,…,Mn满足线性方程组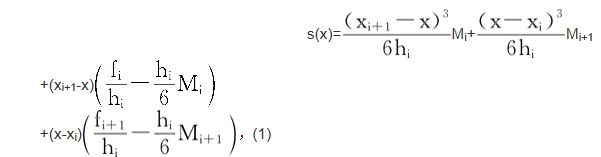
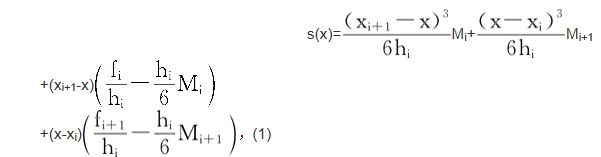
hi-1Mi-1+2(hi-1+hi)Mi+hiMi+1
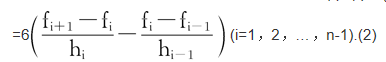
方程组(2)是含有n+1个未知数Mi(i=0,1,…,n)的由n-1个方程组成的线性方程组,不能定解.为此尚需补充两个条件.一般,在插值区间两个端点各补充一个条件,通常称为端点条件.最常用的端点条件有三种类型:
1.s′(x0)=f0′, s′(xn)=fn′.
2.s″(x0)=f0″, s″(xn)=fn″.
3.s(x0)=s(xn) (j=0,1,2).
用Mi表示,这三种条件依次为:

求解过程
1.将方程组(2)与三种端点条件的任何一种联合,解关于M0,M1,…,Mn的线性方程组.
2.将Mi(i=0,1,…,n)代入方程组(1)就得到s(x)关于各子区间的表达式.
特别指出,若第2种端点条件取为
M0=Mn=0(s″(x0)=s″(xn)=0),
据此得到的样条插值函式称为自然样条,它在理论上,计算实践上都是很重要的.上面求解三次样条插值的方法称为三弯矩法,是三次样条插值解算方法中最常用的一种。
三次样条函式的构造
在工程上,构造三次样条插值函式通常有两种方法:一是以给定插值结点处得二阶导数值作为未知数来求解,而工程上称二阶导数为弯矩,因此,这种方法成为三弯矩插值。二是以给定插值结点处得一阶导数作为未知数来求解,而一阶导数又称为斜率,因此,这种方法称为三斜率插值。
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯