拉普拉斯分布
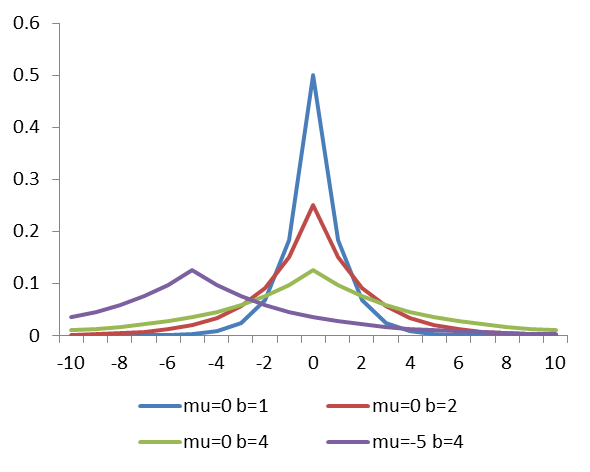
如果随机变数的机率密度函式分布如图所示,那幺它就是拉普拉斯分布,记为x-Laplace(μ,b),其中,μ 是位置参数,b 是尺度参数。如果 μ = 0,那幺,正半部分恰好是尺度为 1/b(或者b,看具体指数分布的尺度参数形式) 的指数分布的一半。
基本介绍
- 中文名:拉普拉斯分布
- 外文名:The Laplace distribution
- 提出:拉普拉斯
- 发现时间:1774年
- 领域:数学
- 性质:指数分布
- 参数:位置参数,尺度参数
定义
设随机变数 具有密度函式
具有密度函式

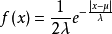
其中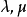 为常数,且
为常数,且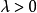 ,则称
,则称 服从参数为
服从参数为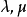 的拉普拉斯分布。
的拉普拉斯分布。
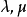
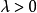

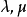
易见,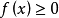 ,且
,且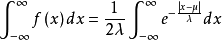 ,
,
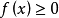
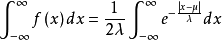
(令 ) =
) =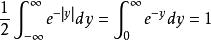 .
.

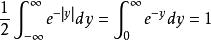
可见
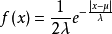
此外
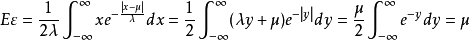
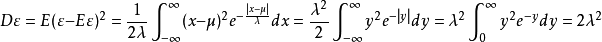
如右图给出了拉普拉斯分布的密度曲线(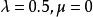 )。
)。 拉普拉斯分布的密度曲线
拉普拉斯分布的密度曲线
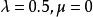
 拉普拉斯分布的密度曲线
拉普拉斯分布的密度曲线拉普拉斯分布的若干性质
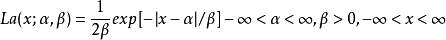
则称X服从参数为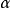 (位置参数)和
(位置参数)和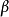 (尺度参数)的拉普拉斯(Laplace)分布,记作
(尺度参数)的拉普拉斯(Laplace)分布,记作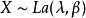 .
.
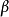
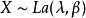
1.拉普拉斯分布的密度函式如式(1)关于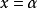 对称,且在该点达到极大值
对称,且在该点达到极大值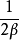 ,即是它的众数。
,即是它的众数。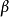 越小曲线越陡,
越小曲线越陡,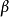 越大曲线越平坦。它有两个拐点
越大曲线越平坦。它有两个拐点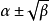 。
。
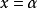
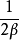
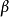
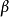
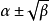
2.设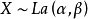 ,则它的分布函式为
,则它的分布函式为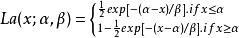 .
.
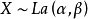
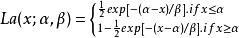
3.设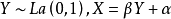 ,则
,则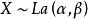 .
.
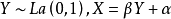
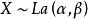
4..设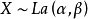 ,则它的r阶中心矩为
,则它的r阶中心矩为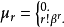 当r为奇数是其值为0,为偶数时其值为
当r为奇数是其值为0,为偶数时其值为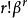 。
。
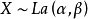
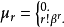
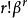
5.设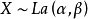 ,则
,则
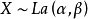
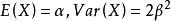
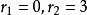
6.设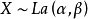 ,则它的矩母函式和特徵函式为
,则它的矩母函式和特徵函式为 ,
, 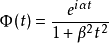 .
.
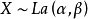

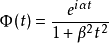
套用
在近代统计中,稳健性占有重要的地位,例如在古典回归分析中,用偏差平方和的大小作标準,来选择回归係数使它达到极小,这种回归不具有稳健性,然而,如改为用偏差的绝对值和作为标準,却具有稳健性.。于是研究随机变数绝对值的分布是很有意义的. 设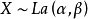 ,可以证明
,可以证明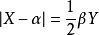 ,其中
,其中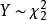 这是一个很有意思的结果。若X与Y独立同分布于
这是一个很有意思的结果。若X与Y独立同分布于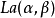 ,则
,则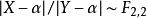 ,上述两个事实表明,若在回归分析中假定服从拉普拉斯分布,并用绝对偏差和作为标準,可以导出很多良好的性质。
,上述两个事实表明,若在回归分析中假定服从拉普拉斯分布,并用绝对偏差和作为标準,可以导出很多良好的性质。
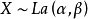
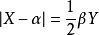
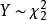
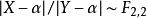
拉普拉斯分布与常态分配有一定的联繫。 设 X , Y , Z ,W 独立同分布于N(0,1),则
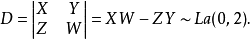
拉普拉斯分布和哥西分布之间有着非常有趣的联繫。C (0,1) 的分布密度和特徵函式 分别为
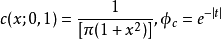
而 的分布密度和持征函式分别是
的分布密度和持征函式分别是
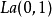
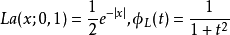
我们看到,C(0,1)的分布密度与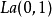 的特徵函式有相同的形式 (仅差一个常数) ,而C (0,1)的特徵函式与
的特徵函式有相同的形式 (仅差一个常数) ,而C (0,1)的特徵函式与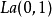 的分布密度也有相同的性质(仅差一个常数) 。
的分布密度也有相同的性质(仅差一个常数) 。
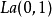
设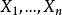 是总体
是总体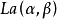 的样本,欲通过它们来估计
的样本,欲通过它们来估计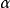 和
和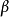 ,将
,将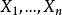 重排得
重排得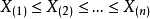 ,若n为奇数,用
,若n为奇数,用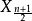 作为
作为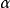 的估计;若n为偶数,则可用
的估计;若n为偶数,则可用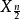 至
至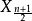 之间的任何一个数来作为
之间的任何一个数来作为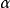 的估计,通常用
的估计,通常用
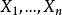
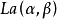
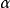
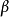
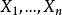
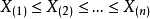
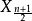
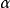
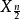
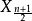
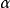
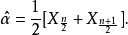
而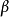 的估计是:
的估计是:
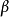
若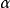 已知,则
已知,则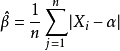
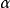
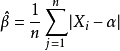
若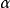 未知,则
未知,则

 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯