梅林变换
在数学中,梅林变换是一种以幂函式为核的积分变换。
基本介绍
- 中文名:梅林变换
- 外文名:Mellin transform
- 分类:积分变换、複分析
- 领域:数理科学
定义
定义式如下:
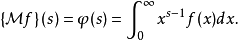
而其逆变换为
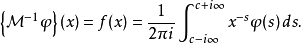
与其他变换之关係
双边拉普拉斯变换
双边拉普拉斯变换可以用梅林变换来表示,如下式
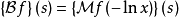
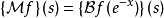
傅立叶变换
傅立叶变换可以用梅林变换来表示,如下式
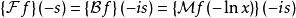
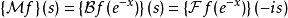
範例
Cahen–Mellin 积分
对于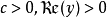 ,且
,且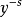 在主要分支(principal branch)上,我们有
在主要分支(principal branch)上,我们有
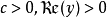
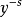
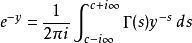
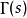
数论
假设
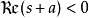
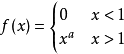
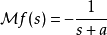
圆柱坐标系下的拉普拉斯运算元
在任何维度的圆柱坐标系中,拉普拉斯运算元总是会包含下式
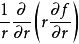
例如,拉普拉斯运算元在二维空间的极坐标表示法

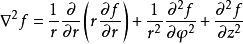
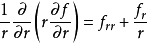
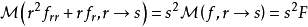
举例来说,二维拉普拉斯方程的极坐标表示法具有以下形式
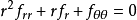
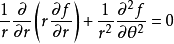
利用梅林变换,可以转换成一个简谐振子的形式
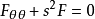
通解为:
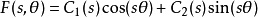
给定边界条件
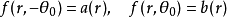
其梅林变换为
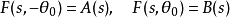
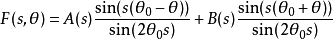
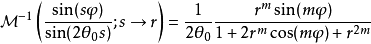
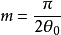
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯