
无条件收敛级数
无条件收敛级数(unconditionally convergentseries)主要包括数值级数的无条件收敛和Banach空间内级数的无条件收敛,两者的定义是相同的,是指任何重排均收敛的级数。换句话说,无条件收敛级数是这样的级数:不管如何交换它的项的次序,所得到的级数仍然收敛,因此,又称可换收敛级数。对数项级数而言,级数是无条件收敛的若且唯若级数是绝对收敛等价的。无穷维空间内的无条件收敛主要包括Hilbert空间内的无条件收敛、Lp空间内的无条件收敛、一致凸Banach空间内的无条件收敛、cotype p的Banach空间内的无条件收敛级数。
基本介绍
- 中文名:无条件收敛级数
- 外文名:unconditionally convergentseries
- 别名:可换收敛级数
- 对象:数值级数、Banach空间内级数
- 定义:任何重排均收敛的级数
- 套用学科:无穷维Banach空间内级数重排
定义
针对数值级数
对于一个无条件收敛级数,把级数的各项相加的顺序做任意的排列后所得到的各种级数仍收敛于同一极限。对数项级数而言,级数是无条件收敛的若且唯若级数是绝对收敛等价的。
在数项级数中,绝对收敛级数主要有两个重要性质:
(1)级数的重排。若数项级数绝对收敛,其和等于S,则任意重排后所得到的级数也绝对收敛且有相同的和数。
(2)级数的乘积。若两级数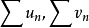 均为绝对收敛级数且分别收敛于A,B,则这两个级数的乘积按正方形顺序或按对角线顺序排列所得的级数也是绝对收敛的,并且收敛于AB。
均为绝对收敛级数且分别收敛于A,B,则这两个级数的乘积按正方形顺序或按对角线顺序排列所得的级数也是绝对收敛的,并且收敛于AB。
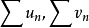
针对Banach空间内级数
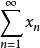
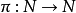
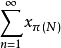
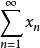
针对泛函级数
假如对任意基本函式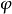 ,级数
,级数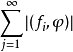 收敛,则称泛函级数
收敛,则称泛函级数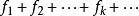 为无条件收敛的。
为无条件收敛的。
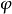
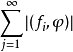
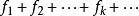
Hilbert空间内的无条件收敛
定理1
设X为Banach空间,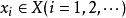 ,则级数
,则级数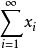 无条件收敛的充要条件是它的任一子级数收敛。
无条件收敛的充要条件是它的任一子级数收敛。
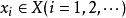
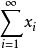
定理2
设Hilbert空间内的级数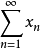 是无条件收敛的,则
是无条件收敛的,则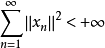 。
。
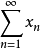
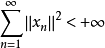
Lp空间内的无条件收敛
设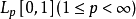 空间内的级数
空间内的级数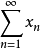 是无条件收敛,则对任何
是无条件收敛,则对任何 ,级数
,级数 收敛。
收敛。
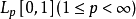
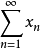


引理
设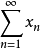 是Banach空间内的无条件收敛级数,则存在常数M>0,对一切的
是Banach空间内的无条件收敛级数,则存在常数M>0,对一切的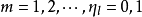 有如下结论成立:
有如下结论成立: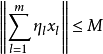 。
。
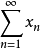
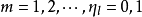
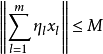
W.Orlicz定理
如果级数 是
是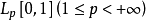 空间内的无条件收敛级数,则有:
空间内的无条件收敛级数,则有:

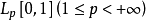
(1)当时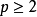 ,
,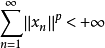 ;
;
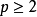
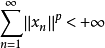
(2)当时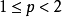 ,
,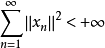 。
。
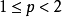
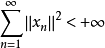
一致凸Banach空间内的无条件收敛
设级数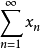 是Banach空间内的无条件收敛级数,则对任何的
是Banach空间内的无条件收敛级数,则对任何的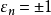 ,级数
,级数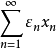 是收敛的。
是收敛的。
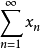
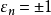
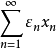
凸性模
在一致凸的Banach空间内,被单位球所截得的距球心距离是 平面直径集合的上界记为
平面直径集合的上界记为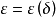 ,它的反函式
,它的反函式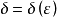 称为空间的凸性模。
称为空间的凸性模。

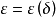
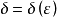
M.H.Kaneu定理
如果级数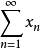 在一致凸Banach空间内是无条件收敛的,其凸性模
在一致凸Banach空间内是无条件收敛的,其凸性模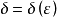 ,则有:
,则有: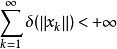 。
。
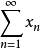
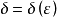
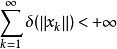
cotype p的Banach空间内的无条件收敛级数
cotype p的Banach空间内的无条件收敛级数的最新结果,包含了着名的W.orlicz的定理。
定理1
设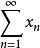 是具有cotype p的Banach空间内的无条件收敛级数,则
是具有cotype p的Banach空间内的无条件收敛级数,则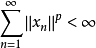 。
。
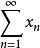
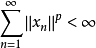
定理2
设 是
是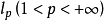 空间内的无条件收敛级数,则有:
空间内的无条件收敛级数,则有:

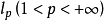
(1)当时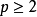 ,
,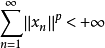 ;
;
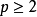
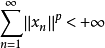
(2)当时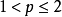 ,
,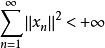 。
。
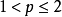
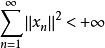
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯