读书笔记摘抄新闻资讯二次根式
一般地，形如√a的代数式叫做二次根式，其中，a 叫做被开方数。当a≥0时，√a表示a的算术平方根；当a小于0时，√a的值为纯虚数（在一元二次方程求根公式中，若根号下为负数，则方程有两个共轭虚根）。判断一个二次根式是否为最简二次根式主要方法是根据最简二次根式的定义进行，或直观地观察被开方数的每一个因数（或因式）的指数都小于根指数2，且被开方数中不含有分母，被开方数是多项式时要先因式分解后再观察。
基本介绍
- 中文名：二次根式
- 外文名：quadratic radical
- 套用：化简二次根式
- 条件：被开方数可以为正为负为0
- 使用领域：初等代数
- 套用学科：数学
定义
定义
如果一个数的平方等于a，那幺这个数叫做a的平方根。a可以是具体的数，也可以是含有字母的代数式。
即：若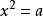
，则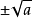
叫做a的平方根，记作x=
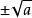。其中a叫被开方数。其中正的平方根被称为算术平方根。
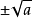
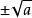
关于二次根式概念，应注意：
被开方数可以是数 ，也可以是代数式。被开方数为正或0的，其平方根为实数；被开方数为负的，其平方根为虚数。
最简二次根式
最简二次根式条件：
1.被开方数的因数是整数或字母，因式是整式；
2.被开方数中不含有可化为平方数或平方式的因数或因式。
二次根式化简一般步骤：
1.把带分数或小数化成假分数；
2.把开方数分解成质因数或分解因式；
3.把根号内能开得尽方的因式或因数移到根号外；
4.化去根号内的分母，或化去分母中的根号；
5.约分。
算术平方根
非负数
的平方根统称为算术平方根，用
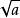（a≥0）来表示。
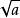
负数没有算术平方根，0的算术平方根为0。
性质
1. 任何一个正数的平方根有两个，它们互为相反数。如正数a的算术平方根是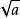
，则a的另一个平方根为﹣
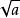；最简形式中被开方数不能有分母存在。
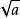
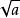
2. 零的平方根是零，即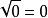
；
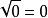
3. 负数的平方根也有两个，它们是共轭的。如负数a的平方根是
。
4. 有理化根式：如果两个含有根式的代数式的积不再含有根式，那幺这两个代数式互为有理化根式，也称互为有理化因式。
5. 无理数可用连分数形式表示，如: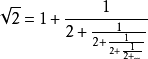
。
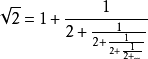
6. 当a≥0时，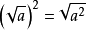
；
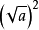与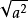
中a取值範围是整个複平面。
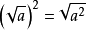
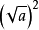
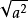
7.
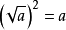[任何一个数都可以写成一个数的平方的形式；利用此性质可以进行因式分解。
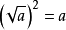
8. 逆用可将根号外的非负因式移到括弧内，如
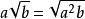
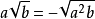
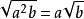
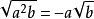
9.注意：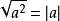
，然后根据绝对值的运算去除绝对值符号。
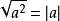
10.具有双重非负性，即不仅a≥0而且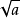
≥0。
有理化因式
两个含有二次根式的代数式相乘，如果他们的积不含有二次根式，那幺这两个代数式叫做互为有理化因式。
注意：①他们必须是成对出现的两个代数式；②这两个代数式都含有二次根式；③这两个代数式的积化简后不再含有二次根式；④一个二次根式可以与几个二次根式互为有理化因式。
常用有理化因式有:
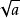
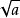
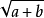
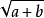
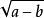
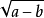
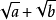
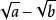
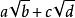
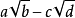
分母有理化
在分母含有根号的式子中，把分母的根号化去，叫做分母有理化。
分母有理化即将分母从非有理数转化为有理数的过程，以下列出分母有理化的几种方法：
1.直接利用二次根式的运算法则：
例：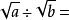
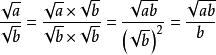﹙b不为0﹚
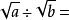
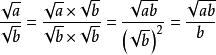
2.利用平方差公式：
例：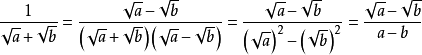
﹙a≠b﹚
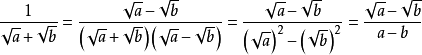
3.利用因式分解：
例：
（此题可运用待定係数法便于分子的分解）
4.利用约分：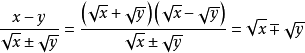
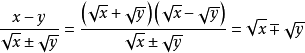
﹙x，y不同时为0﹚
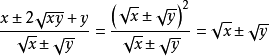
﹙x，y不同时为0﹚
分子有理化
把分子中的根号化去，叫做分子有理化。
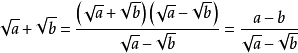
换元法
换元法即把根式中的某一部分用另一个字母代替的方法，是化简的重要方法之一。
例：在根式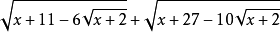
中，令
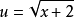，即可得到
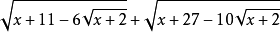
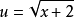
（此处，x>=-2,u>=0）
当0<=u<=3时，则-2<=x<=7
原式=3-u + 5-u =8-2u；
当3<=u<=5时，则7<=x<=23
原式=u-3 +5-u =2；
当u>=5时，x>=23
原式=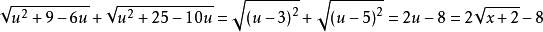
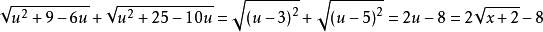
分析：通过换元法换元，将根号下的数化简，最后求值。
运算
加减法
1.同类二次根式
一般地，把几个二次根式化为最简二次根式后，如果它们的被开方数相同，就把这几个二次根式叫做同类二次根式。 化简：根号12等于4的根号3
2.合併同类二次根式
把几个同类二次根式合併为一个二次根式就叫做合併同类二次根式。
3.二次根式加减时，可以先将二次根式化为最简二次根式，再将被开方数相同的进行合併。
例如：（1）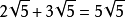
；（2）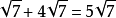
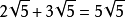
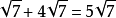
乘除法
二次根式相乘除，把被开方数相乘除，根指数不变，再把结果化为最简二次根式。
1.乘法运算
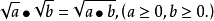
用语言叙述为：两个数的算术平方根的积，等于这两个因式积的算术平方根。
推广
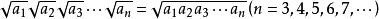
（a≥0，b≥0）
2.除法运算
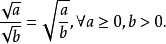
用语言叙述为：两个数的算术平方根的商，等于这两个数商的算术平方根。
推广
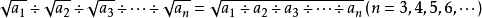
（a≥0，b>0）
混合运算
二次根式混合运算与实数运算相同的运算顺序相同，先乘方，在乘除，后加减，有括弧的先算括弧里面的。
乘法公式
1.
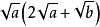型，运用分配律化简，原式
。
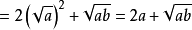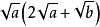
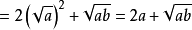
2.
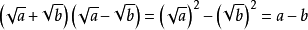， 直接运用平方差公式。
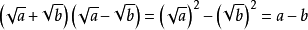
3.
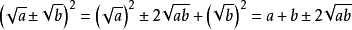， 直接运用完全平方公式。
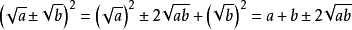
4.
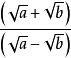型，运用分母有理化运算。
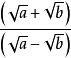
开平方运算
求一个非负数的平方根的运算，叫做开平方。开平方与平方互为逆运算。
运算方法
1.确定运算顺序。
2.灵活运用运算定律。
3.正确使用乘法公式。
4.大多数分母有理化要及时。
5.在有些简便运算中也许可以约分，不要盲目有理化（但最后结果必须是分母有理化的）。
6.字母运算时注意隐含条件和末尾括弧的注明。
7.提公因式时可以考虑提带根号的公因式。
套用
二次根式的套用主要体现在两个方面：
（1）利用从特殊到一般，再由一般到特殊的重要思想方法，解决一些规律探索性问题；
（2）利用二次根式解决长度、高度计算问题，根据已知量，求出一些长度或高度，或设计省料的方案，以及图形的拼接、分割问题。这个过程需要用到二次根式的计算，其实就是化简求值。
共轭根式
共轭根式
当A，B，C，D都是有理式，而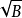
,
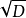中至少有一个是无理式时，称
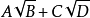和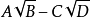
互为共轭根式。这两式的积是有理式
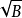
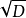
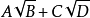
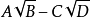
两个根式互为共轭根式，则他们互为有理化因式。
共轭虚根（证明）
【共轭】定义：複数中，实部相等，而虚部互为相反数的一对複数，称为共轭複数对。
形如：a+bi 和a-bi
【求根公式】：
对于任意一个一元二次方程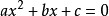
，它的两个根是 ：
,
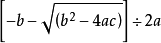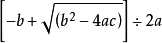。这是由配方法求得的公式。
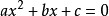
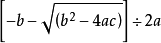
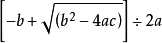
当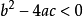
时，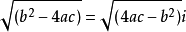
。
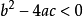
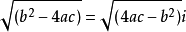
所以，方程的两个根就变为 ：
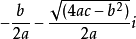
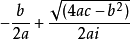
这样，两根的实部都为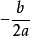
，两根的虚部
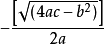和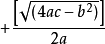
互为相反数，两根就成为了共轭的一对复根。
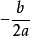
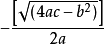
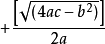
两个实部相等，虚部互为相反数的複数互为共轭複数（conjugate complex number）（当虚部不等于0时也叫共轭虚数）。複数z的共轭複数记作z'。
根据定义，若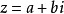
（
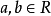），则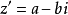
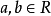（ ）。即共轭複数所对应的点关于实轴对称。
1.代数特徵：
（1）
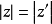
（2）
（实数），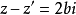
（3）
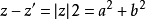（为一实数）
（4）
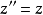
2.运算特徵：
（1）
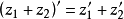
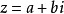
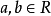
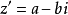
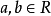
1.代数特徵：
（1）
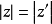
（2）
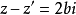
（3）
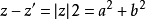
（4）
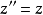
2.运算特徵：
（1）
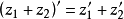
（2）
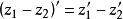
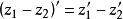
（3）
（4）
(
)
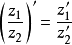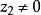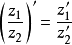
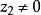
3.模的运算性质：
（1）
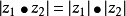
（1）
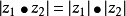
（2）
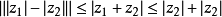
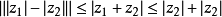
（3）
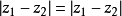，是複平面的两点间距离公式，由此几何意义可以推出複平面上的直线、圆、双曲线、椭圆的方程以及抛物线。
注意：z′表示複数z的共轭複数（实际形式为z上一横），z″表示複数z的共轭複数的共轭複数（为z上两横）。
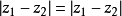
注意：z′表示複数z的共轭複数（实际形式为z上一横），z″表示複数z的共轭複数的共轭複数（为z上两横）。