根式
根式是数学的基本概念之一,是一种含有开方(求方根)运算的代数式,即含有根号的表达式。按根指数是偶数还是奇数,根式分别称为偶次根式或奇次根式。
基本介绍
- 中文名:根式
- 外文名:radical expression
- 类型:代数运算
- 所属学科:数学
- 分类:偶次根式、奇次根式
定义
设正整数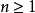 ,已知数a,若有数x满足
,已知数a,若有数x满足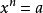 ,则称x为a的n次方根,记为
,则称x为a的n次方根,记为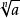 当n=2时,记为
当n=2时,记为 ,作为代数式,
,作为代数式,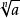 称为根式,n称为根指数,a称为根底数。在实数範围内,负数不能开方,一个正数开偶次方有两个根,其绝对值相等,符号相反。
称为根式,n称为根指数,a称为根底数。在实数範围内,负数不能开方,一个正数开偶次方有两个根,其绝对值相等,符号相反。
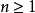
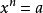
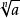

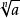
根式的性质
①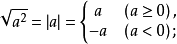
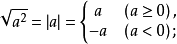
②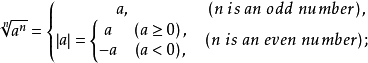
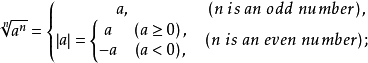
③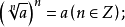
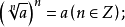
④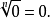
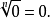
n次算术根
若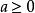 ,则称
,则称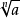 为a的n次算数根。算术根是唯一的,且是非负数的非负方根。
为a的n次算数根。算术根是唯一的,且是非负数的非负方根。
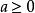
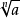
同次根式
跟指数相同的根式。只有同次根式才能进行乘、除运算。
同类根式
被开方数相同、根指数也相同的根式。只有同类根式才能进行加、减运算。
根式的运算法则
①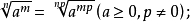
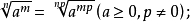
②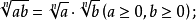
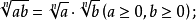
③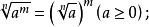
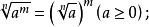
④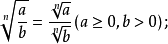
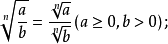
⑤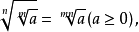 其中
其中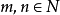 .
.
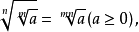
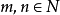
最简根式
当根式满足以下三个条件时,称为最简根式。
①被开方数的指数与根指数互质;
②被开方数不含分母,即被开方数中因数是整数,因式是整式;
③被开方数中不含开得尽方的因数或因式。
分母有理化
又称“有理化分母”,是指通过适当的变形划去代数式分母中根号的运算。
一般情况下,在进行根式运算及把一个根式化成最简根式时,都要将分母有理化,两个含有根式的代数式相乘,如果它们的积不含根号,我们就说这两个代数式互为有理化因式。
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯