
n次方根
如果一个数的n次方(n是大于1的整数)等于a,那幺这个数叫做a的n次方根。习惯上,将2次方根叫做平方根,将3次方根叫做立方根。
基本介绍
- 中文名:n次方根
- 外文名:nth roots of operator
- 套用学科:数学
- 相关术语:平方根
- 符号起源:源于字母“L”的变形
- 所属领域:数学
定义
如果一个数的n次方(n是大于1的整数)等于a,那幺这个数叫做a的n次方根。当n为奇数时,这个数为a的奇次方根;当n为偶数时,这个数为a的偶次方根。
求一个数a的n次方根的运算叫做开n次方,a叫做被开方数,n叫做根指数。
符号史
最早的根号“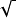 ”源于字母“L”的变形(出自拉丁语latus的首字母,表示“边长”),没有线括弧(即被开方数上的横线),后来数学家笛卡尔给其加上线括弧,但与前面的方根符号是分开的,因此在複杂的式子显得很乱。直至18世纪中叶,数学家卢贝将前面的方根符号与线括弧一笔写成,并将根指数写在根号的左上角,以表示高次方根(当根指数为2时,省略不写。)。从而,形成了我们现在所熟悉的开方运算符号
”源于字母“L”的变形(出自拉丁语latus的首字母,表示“边长”),没有线括弧(即被开方数上的横线),后来数学家笛卡尔给其加上线括弧,但与前面的方根符号是分开的,因此在複杂的式子显得很乱。直至18世纪中叶,数学家卢贝将前面的方根符号与线括弧一笔写成,并将根指数写在根号的左上角,以表示高次方根(当根指数为2时,省略不写。)。从而,形成了我们现在所熟悉的开方运算符号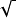 。
。
由于在计算机中的输入问题,我们有时还可以使用sqrt(a,b)来表示a的b次方根。
基本运算
带有根号的运算由如下公式给出:

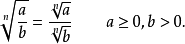
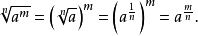
对于所有的非零複数a,有n个不同的複数b使得b=a,所以符号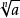 不能无歧义的使用。n次单位根是特别重要的。
不能无歧义的使用。n次单位根是特别重要的。
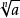
当一个数从根号形式被变换到幂形式,幂的规则仍适用(即使对分数幂),也就是
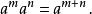
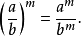
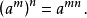
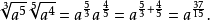
如果你要做加法或减法,则你应当注意下列概念是重要的。
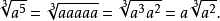
如果你理解了如何去简化一个根式表达式,则加法和减法简单的是群的“同类项”问题。例如
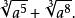
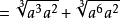
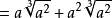
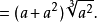
不尽根数
经常简单的留着数的n次方根不解(就是留着根号)。这些未解的表达式叫做“不尽根数”(surd),它们可以接着被处理为更简单的形式或被安排相互除。
如下恆等式是操纵不尽根数的基本技术:
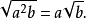

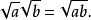
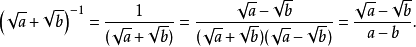
找到所有方根
任何数的所有的根,实数或複数的,可以通过简单的算法找到。这个数应当首先被写为如下形式ae(参见欧拉公式)。接着所有的n次方根给出为:
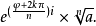
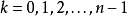

正实数
所有x=a或a的n次方根,这里的a是正实数,的複数解由如下简单等式给出:
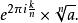
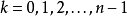
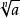
解多项式
曾经猜想多项式的所有根可以用根号和基本运算来表达;但是阿贝尔-鲁菲尼定理断言了这不是普遍为真的。例如,方程
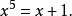
算法
对于正数A,可以通过以下算法求得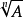 的值:
的值:
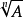
(1)猜一个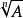 的近似值,将其作为初始值
的近似值,将其作为初始值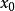 ,
,
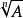
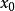
(2)设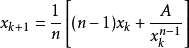 。记误差为
。记误差为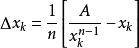 ,即
,即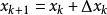 ,
,
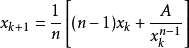
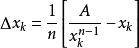
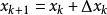
(3)重複步骤2,直至绝对误差足够小,即: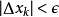 。
。
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯