
点(数学概念)
点是最简单的形,是几何图形最基本的组成部分。在空间中作为 1 个 0 维的对象。在其他领域中,点也作为讨论的对象。
在欧氏几何中,点是空间中只有位置,没有大小的图形。点是整个欧氏几何的基础。欧几里得最初含糊地定义点作为"没有部分的东西"。在二维欧氏空间中,1 个点被表示为 1 组有序数对。同样的,在笛卡尔坐标系中,任意 1 个点都可以被精确地定位。
在现代数学语言中,任何集合的元素都叫作“点”,但与三维空间中的点可以没有任何关係。
基本介绍
- 中文名:点
- 外文名:Point
- 通用学科:科学、数学、哲学
- 通用领域:几何学、拓扑学、分形、矢量图形
- 拼音:diǎn
定义无效
点是无法被定义的。试图去定义点就会陷入重複定义、逆逻辑定义的深渊。点作为原始概念的同时也具有原始概念的性质。
在科学系统中总是要对概念下定义,而且一定会用一些已知的概念来定义新的概念,但概念的个数是有限的,又由第二条规则可知,下定义是不能恶性循环的,因此总有一些概念不能引用别的概念来定义,这样概念叫做这个科学体系中的原始概念。
比如,把平行四边形定义为两组对边分别平行的四边形,因此就必须先对四边形、平行以及对边进行定义。定义四边形时,应先对多边形及边进行定义,又必须先定义折线,故必须先要对点和直线进行定义。但是,在一般的初等几何中,点和直线都无法再用已被定义过的概念进行定义,它们都是原始概念。在数学中,点、直线、平面、集合,空间、数、量等都是原始概念,但在其中有些是通过公理来直接描述的,虽然有些概念在中学课本中也有解释,但这种解释并不是定义。
点的含义
在几何学、拓扑学以及数学的相关分支中,空间中的点用于描述给定空间中的 1 种特别的对象,在空间中有类似于体积、面积、长、宽、高的类似物。1 个点是 1 个 0 维的对象。点作为最简单的图形概念,通常作为几何学、物理学、矢量图形和其他领域中最基本的组成部分。
点的历史
在亚里斯多德的着作【论天体】第三册中,已经提到数学中的点是没有大小的,他依此来驳斥柏拉图将数学的几何形视为物理实体的构成要素(参见正多面体),并强调这与当时的数学定义相违背:数学的平面没有厚度,所以不能构造物理实体。他论述说,如果数学平面有厚度,那幺数学的线就要有宽度才能够构成平面,而数学的点必须有大小才能构成线,但是在数学中已经明确定义数学的点是没有大小的,因此柏拉图的理论与数学相牴触。从这里,亚里斯多德陈述说,一个几何物件只能分割成相同型态的几何物件(而不会变成其它的东西):平面只能分割成平面,而不能分割成线;线只能分割成线,不能分割成点;这样的分割可以无限的进行,而不是像原子论者所说的,最后分割到原子(或是基本构成要素)就停止了。
因此,早在欧几里得的【几何原本】之前,数学中的点只用来标示位置的用法已经是共识。亚里斯多德提到点的时候,用的字是 στιγμὰς,是可见的点(spot),而欧几里得则(小心翼翼的)採用另一个字 σημεῖόν,原意是“标示”(sign):
σημεῖόν ἐστιν, οὗ μέρος οὐθέν.
这句话的意思是:点是没有部分(μέρος)的东西。点没有部分,所以也就没有大小。这个论点来源自亚里斯多德的“部分-整体”理论(part–whole theory):
"the parts are causes of the whole"(整体是由部分所构成的。)
【几何原本】的阿拉伯文版,将 σημεῖόν 翻译为 نقطة,意思回到亚里斯多德的可见点;拉丁文版则将 σημεῖόν 翻译为 punctum,意思是被尖物刺成的小洞。
特殊的点
(内容待补充)
端点:1 条线段两端上的点或1条射线一端上的点(即线段或射线的起点或终点);

等分点:把 1 条线段平均分成若干条线段的点;
顶点:图形的边的公共点;
交点:两条直线的公共点。
点的性质
- 不可定义性:定义无效;
- 确定性:任意 1 个点都可以用有序数对精确地定位;
- 唯一性:1 组有序数对能且只能定位 1 个点;
- 互异性:任意两个点都是不同的对象。
点到点的距离
点 A(x,y,z)到点 B(x2,y2,z2)的距离为
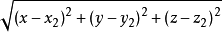
位置关係
点和点
- 点和点重合;
- 点和点不重合。
点和直线
- 点在直线上;
- 点在直线外。
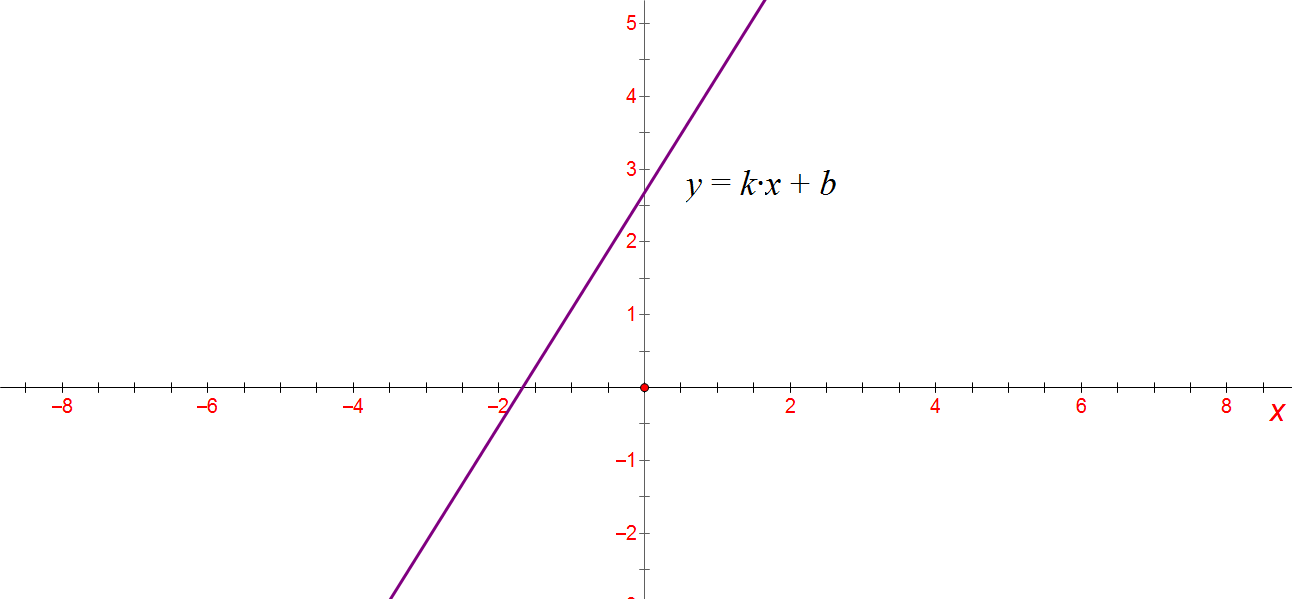
点和平面
- 点在平面上;
- 点在平面外。
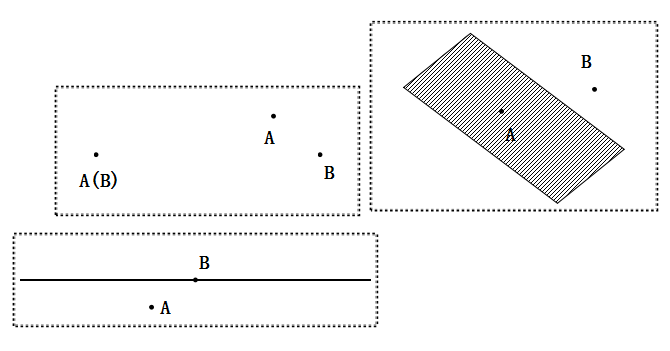
点的平移
点左右平移只影响横坐标的变化,点上下平移只影响纵坐标的变化:
设点A的坐标为(x,y).
1若把点A向左平移k(k>0)个单位后,坐标变为(x-k,y);若把点A向右平移k个单位后,坐标则变为(x+k,y).
2.若把点A向上平移k(k>0)个单位后,坐标变为(x,y+k);若把点A向下平移k个单位后,坐标则变为(x,y-k).
3.若把点A先向左平移p个单位,再向上平移q个单位,坐标则变为(x-p,y+q).

点的对称
点 A(x,y,z)关于点 B(x2,y2,z2)的对称点的坐标

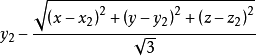
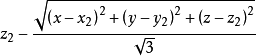
点的旋转
(内容待补充)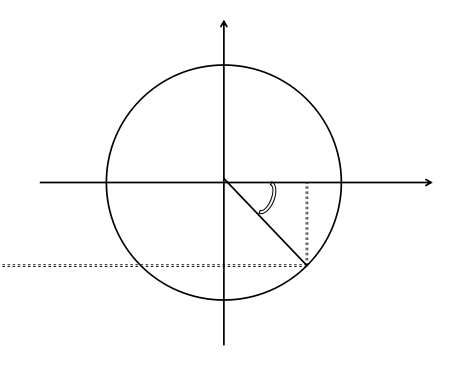

点 A(x,y,z)绕原点旋转 n°后的位置特徵:
点 A(x,y,z)绕点 B(x2,y2,z2)旋转 n°后的位置特徵:
其他的点
点集拓扑中的点定义为拓扑空间中的集合的元素。
儘管点被看做几何学和拓扑学中的基本概念,但是有些几何和拓扑理论并不需要点的概念,例如非交换几何和非点集拓扑,1 个"非点空间"不是作为 1 个集合来定义的,而是通过某种类似于函式空间的结构。(代数上的或逻辑上的连续函式代数或集合代数。)
错误理解
线段是由无限个点构成的,而线段的长度让人们错误的认为点是有长度或者长度是无穷小。但这是严重错误的。因为这违背了测度论和点的基本属性。点的长度是 0 而不是无穷小。
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯