
数学期望
在机率论和统计学中,数学期望(mean)(或均值,亦简称期望)是试验中每次可能结果的机率乘以其结果的总和,是最基本的数学特徵之一。它反映随机变数平均取值的大小。
需要注意的是,期望值并不一定等同于常识中的“期望”——“期望值”也许与每一个结果都不相等。期望值是该变数输出值的平均数。期望值并不一定包含于变数的输出值集合里。
大数定律规定,随着重複次数接近无穷大,数值的算术平均值几乎肯定地收敛于期望值。
基本介绍
- 中文名:数学期望
- 外文名:Expectation
- 别称:均值,期望
- 表达式:E(x)
- 套用学科:数学
- 适用领域範围:数学统计;数据挖掘
- 基本释义:该变数输出值的平均数
历史故事
在17世纪,有一个赌徒向法国着名数学家帕斯卡挑战,给他出了一道题目:甲乙两个人赌博,他们两人获胜的机率相等,比赛规则是先胜三局者为赢家,一共进行五局,赢家可以获得100法郎的奖励。当比赛进行到第四局的时候,甲胜了两局,乙胜了一局,这时由于某些原因中止了比赛,那幺如何分配这100法郎才比较公平?
用机率论的知识,不难得知,甲获胜的可能性大,乙获胜的可能性小。
因为甲输掉后两局的可能性只有(1/2)×(1/2)=1/4,也就是说甲赢得后两局的机率为1-(1/4)=3/4,甲有75%的期望获得100法郎;而乙期望赢得100法郎就得在后两局均击败甲,乙连续赢得后两局的机率为(1/2)*(1/2)=1/4,即乙有25%的期望获得100法郎奖金。
可见,虽然不能再进行比赛,但依据上述可能性推断,甲乙双方最终胜利的客观期望分别为75%和25%,因此甲应分得奖金的100*75%=75(法郎),乙应分得奖金的的100×25%=25(法郎)。这个故事里出现了“期望”这个词,数学期望由此而来。
离散型
如果随机变数只取得有限个值或无穷能按一定次序一一列出,其值域为一个或若干个有限或无限区间,这样的随机变数称为离散型随机变数。
离散型随机变数的一切可能的取值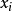 与对应的机率
与对应的机率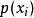 乘积之和称为该离散型随机变数的数学期望(若该求和绝对收敛),记为
乘积之和称为该离散型随机变数的数学期望(若该求和绝对收敛),记为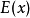 。它是简单算术平均的一种推广,类似加权平均。
。它是简单算术平均的一种推广,类似加权平均。
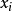
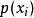
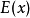
公式
离散型随机变数X的取值为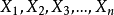 ,
,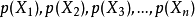 为X对应取值的机率,可理解为数据
为X对应取值的机率,可理解为数据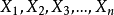 出现的频率
出现的频率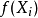 ,则:
,则:
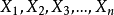
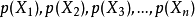
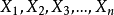
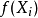
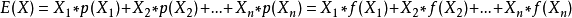
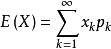
例子
某城市有10万个家庭,没有孩子的家庭有1000个,有一个孩子的家庭有9万个,有两个孩子的家庭有6000个,有3个孩子的家庭有3000个。
则此城市中任一个家庭中孩子的数目是一个随机变数,记为X。它可取值0,1,2,3。
其中,X取0的机率为0.01,取1的机率为0.9,取2的机率为0.06,取3的机率为0.03。
则,它的数学期望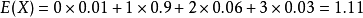 ,即此城市一个家庭平均有小孩1.11个,当然人不可能用1.11个来算,约等于2个。
,即此城市一个家庭平均有小孩1.11个,当然人不可能用1.11个来算,约等于2个。
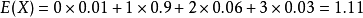
设Y是随机变数X的函式: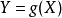 (
(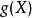 是连续函式)
是连续函式)
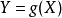
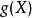
它的分布律为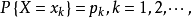 若
若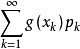 绝对收敛,则有:
绝对收敛,则有:
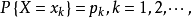
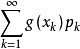
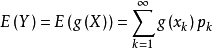
连续型
设连续性随机变数X的机率密度函式为f(x),若积分绝对收敛,则称积分的值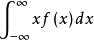 为随机变数的数学期望,记为E(X)。
为随机变数的数学期望,记为E(X)。
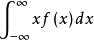
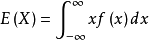
若随机变数X的分布函式F(x)可表示成一个非负可积函式f(x)的积分,则称X为连续性随机变数,f(x)称为X的机率密度函式(分布密度函式)。
数学期望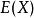 完全由随机变数X的机率分布所确定。若X服从某一分布,也称
完全由随机变数X的机率分布所确定。若X服从某一分布,也称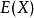 是这一分布的数学期望。
是这一分布的数学期望。
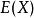
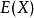
定理
若随机变数Y符合函式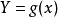 ,且
,且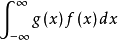 绝对收敛,则有:
绝对收敛,则有:
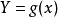
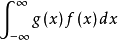
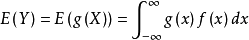
该定理的意义在于:我们求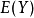 时不需要算出Y的分布律或者机率分布,只要利用X的分布律或机率密度即可。
时不需要算出Y的分布律或者机率分布,只要利用X的分布律或机率密度即可。
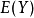
上述定理还可以推广到两个或以上随机变数的函式情况。
设Z是随机变数X、Y的函式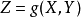 (g是连续函式),Z是一个一维随机变数,二维随机变数(X,Y)的机率密度为
(g是连续函式),Z是一个一维随机变数,二维随机变数(X,Y)的机率密度为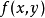 ,则有:
,则有:
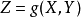
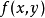

区别
离散型随机变数与连续型随机变数都是由随机变数取值範围(取值)确定。
变数取值只能取离散型的自然数,就是离散型随机变数。例如,一次掷20个硬币,k个硬币正面朝上,k是随机变数。k的取值只能是自然数0,1,2,…,20,而不能取小数3.5、无理数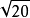 ,因而k是离散型随机变数。
,因而k是离散型随机变数。
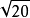
如果变数可以在某个区间内取任一实数,即变数的取值可以是连续的,这随机变数就称为连续型随机变数。例如,公共汽车每15分钟一班,某人在站台等车时间x是个随机变数,x的取值範围是[0,15),它是一个区间,从理论上说在这个区间内可取任一实数3.5、无理数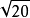 等,因而称这随机变数是连续型随机变数。
等,因而称这随机变数是连续型随机变数。
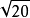
性质
设C为一个常数,X和Y是两个随机变数。以下是数学期望的重要性质:
1.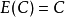
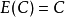
2.

3.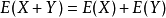
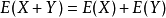
4.当X和Y相互独立时,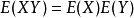
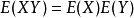
性质3和性质4可以推到到任意有限个相互独立的随机变数之和或之积的情况。
证明:
这里只对连续性随机变数的情况加以证明,对离散型的证明只要将证明中的积分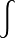 改为和式
改为和式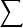 即可。
即可。
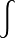
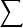
1.永远都只能取C,常数C的平均数还是它本身。
2.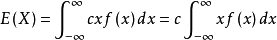
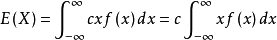
3.设二维随机变数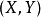 的机率密度函式为
的机率密度函式为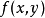 。
。
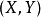
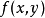

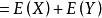
4.若X和Y相互独立,其边缘机率密度函式为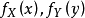 ,有
,有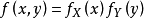
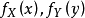
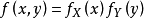
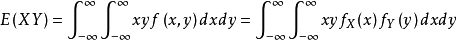
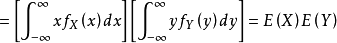
套用
经济决策
假设某一超市出售的某种商品,每周的需求量X在10至30範围内等可能取值,该商品的进货量也在10至30範围内等可能取值(每周只进一次货)超市每销售一单位商品可获利500元,若供大于求,则削价处理,每处理一单位商品亏损100元;若供不应求,可从其他超市调拨,此时超市商品可获利300元。试计算进货量多少时,超市可获得最佳利润?并求出最大利润的期望值。
分析:由于该商品的需求量(销售量)X是一个随机变数,它在区间[10,30]上均匀分布,而销售该商品的利润值Y也是随机变数,它是X的函式,称为随机变数的函式。题中所涉及的最佳利润只能是利润的数学期望(即平均利润的最大值)。因此,本问题的解算过程是先确定Y与X的函式关係,再求出Y的期望E(Y)。最后利用极值法求出E(Y)的极大值点及最大值。
抽奖问题
假设某百货超市现有一批快到期的日用产品急需处理,超市老闆设计了免费抽奖活动来处理掉了这些商品。纸箱中装有大小相同的20个球,10个10分,10个5分,从中摸出10个球,摸出的10个球的分数之和即为中奖分数,获奖如下:
一等奖 100分,冰柜一个,价值2500元;
二等奖 50分, 电视机一个,价值1000元;
三等奖 95分, 洗髮液8瓶,价值178元;
四等奖 55分, 洗髮液4瓶,价值88元;
五等奖 60分, 洗髮液2瓶,价值44元;
六等奖 65分, 牙膏一盒, 价值8元;
七等奖 70分, 洗衣粉一袋,价值5元;
八等奖 85分, 香皂一块, 价值3元;
九等奖 90分, 牙刷一把, 价值2元;
十等奖 75分与80分为优惠奖,只収成本价22元,将获得洗髮液一瓶;
分析:表面上看整个活动对顾客都是有利的,一等奖到九等奖都是白得的,只有十等奖才收取一点成本价。但经过分析可以知道商家真的就亏损了吗?顾客就真能从中获得抽取大奖的机会吗?求得其期望值便可真相大白。摸出10个球的分值只有11种情况,用X表示摸奖者获得的奖励金额数,计算得到E(X)=-10.098,表明商家在平均每一次的抽奖中将获得10.098元,而平均每个抽奖者将花 10.098元来享受这种免费的抽奖。 从而可以看出顾客真的就站到大便宜了吗?相反,商家採用这种方法不仅把快要到期的商品处理出去了,而且还为超市大量集聚了人气,一举多得。此百货超市老闆运用数学期望估计出了他不会亏损而做了这个免费抽奖活动,最后一举多得,从中可看出了数学期望这一科学的方法在经济决策中的重要性。
体育比赛问题
桌球是我们的国球,上世纪兵兵球也为中国带了一些外交。中国队在这项运动中具有绝对的优势。现就桌球比赛的安排提出一个问题:假设德国队(德国队名将波尔在中国也有很多球迷)和中国队比赛。赛制有两种,一种是双方各出3人,三场两胜制, 一种是双方各出5人,五场三胜制,哪一种赛制对中国队更有利?
分析:由于中国队在这项比赛中的优势,不妨设中国队中每一位队员德国队员的胜率都为60%,接着只需要比较两个队对应的数学期望即可。
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯