
集合(数学概念)
集合,简称集,是数学中一个基本概念,也是集合论的主要研究对象。集合论的基本理论创立于19世纪,关于集合的最简单的说法就是在朴素集合论(最原始的集合论)中的定义,即集合是“确定的一堆东西”,集合里的“东西”则称为元素。现代的集合一般被定义为:由一个或多个确定的元素所构成的整体。
基本介绍
- 中文名:集合
- 外文名:aggregate
- 简称:集
- 定义:一个或多个确定元素所构成的整体
- 提出者:康托尔
- 创立时间:19世纪
定义
概念
集合是指具有某种特定性质的具体的或抽象的对象汇总而成的集体。其中,构成集合的这些对象则称为该集合的元素。
例如,全中国人的集合,它的元素就是每一个中国人。通常用大写字母如A,B,S,T,...表示集合,而用小写字母如a,b,x,y,...表示集合的元素。若x是集合S的元素,则称x属于S,记为x∈S。若y不是集合S的元素,则称y不属于S,记为y∉S 。
基数
集合中元素的数目称为集合的基数,集合A的基数记作card(A)。当其为有限大时,集合A称为有限集,反之则为无限集。一般的,把含有有限个元素的集合叫做有限集,含无限个元素的集合叫做无限集。
表示
假设有实数x < y:
①[x,y] :方括弧表示包括边界,即表示x到y之间的数以及x和y;
②(x,y):小括弧是不包括边界,即表示大于x、小于y的数。
地位
集合在数学领域具有无可比拟的特殊重要性。集合论的基础是由德国数学家康托尔在19世纪70年代奠定的,经过一大批科学家半个世纪的努力,到20世纪20年代已确立了其在现代数学理论体系中的基础地位,可以说,现代数学各个分支的几乎所有成果都构筑在严格的集合理论上。
特性
确定性
给定一个集合,任给一个元素,该元素或者属于或者不属于该集合,二者必居其一,不允许有模稜两可的情况出现。
互异性
一个集合中,任何两个元素都认为是不相同的,即每个元素只能出现一次。有时需要对同一元素出现多次的情形进行刻画,可以使用多重集,其中的元素允许出现多次。
无序性
一个集合中,每个元素的地位都是相同的,元素之间是无序的。集合上可以定义序关係,定义了序关係后,元素之间就可以按照序关係排序。但就集合本身的特性而言,元素之间没有必然的序。
分类
空集
有一类特殊的集合,它不包含任何元素,如{x|x∈R x2+1=0} ,称之为空集,记为∅。空集是个特殊的集合,它有2个特点:
- 空集∅是任意一个非空集合的真子集。
- 空集是任何一个集合的子集。
子集
设S,T是两个集合,如果S的所有元素都属于T ,即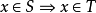 则称S是T的子集,记为
则称S是T的子集,记为 。显然,对任何集合S ,都有
。显然,对任何集合S ,都有 。其中,符号
。其中,符号 读作包含于,表示该符号左边的集合中的元素全部是该符号右边集合的元素。如果S是T的一个子集,即
读作包含于,表示该符号左边的集合中的元素全部是该符号右边集合的元素。如果S是T的一个子集,即 ,但在T中存在一个元素x不属于S ,即
,但在T中存在一个元素x不属于S ,即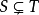 ,则称S是T的一个真子集。
,则称S是T的一个真子集。
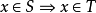




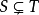
交并集
交集定义:由属于A且属于B的相同元素组成的集合,记作A∩B(或B∩A),读作“A交B”(或“B交A”),即A∩B={x|x∈A,且x∈B}, 如右图所示。注意交集越交越少。若A包含B,则A∩B=B,A∪B=A。 图1 交集与并集
图1 交集与并集
 图1 交集与并集
图1 交集与并集并集定义:由所有属于集合A或属于集合B的元素所组成的集合,记作A∪B(或B∪A),读作“A并B”(或“B并A”),即A∪B={x|x∈A,或x∈B},如右图所示。注意并集越并越多,这与交集的情况正相反。
补集
补集又可分为相对补集和绝对补集。
相对补集定义:由属于A而不属于B的元素组成的集合,称为B关于A的相对补集,记作A-B或A\B,即A-B={x|x∈A,且x∉B'}。
绝对补集定义:A关于全集合U的相对补集称作A的绝对补集,记作A'或∁u(A)或~A。有U'=Φ;Φ'=U。
幂集
设有集合A,由集合A所有子集组成的集合,称为集合A的幂集。对于幂集有定理如下:有限集A的幂集的基数等于2的有限集A的基数次幂。
区间
数学分析中,最常遇到的实数集的子集是区间。
设a,b(a<b)是两个相异的实数,则满足不等式a<x<b的所有实数x的集合称为以a,b为端点的开区间,记为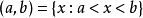 ;满足不等式
;满足不等式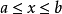 的所有实数的集合称为以a,b为端点的闭区间,记为
的所有实数的集合称为以a,b为端点的闭区间,记为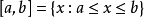 ;满足不等式
;满足不等式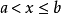 或
或 的所有实数x的集合称为以a,b为端点的半开半闭区间,分别记为
的所有实数x的集合称为以a,b为端点的半开半闭区间,分别记为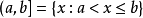 及
及 。除此之外,还有下述几类无限区间:
。除此之外,还有下述几类无限区间:
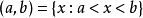
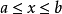
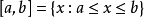
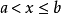

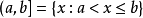



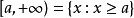
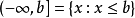

模糊集
用来表达模糊性概念的集合,又称模糊集、模糊子集。普通的集合是指具有某种属性的对象的全体。这种属性所表达的概念应该是清晰的,界限分明的。因此每个对象对于集合的隶属关係也是明确的,非此即彼。但在人们的思维中还有着许多模糊的概念,例如年轻、很大、暖和、傍晚等,这些概念所描述的对象属性不能简单地用“是”或“否”来回答,而模糊集合就是指具有某个模糊概念所描述的属性的对象的全体。
由于概念本身不是清晰的、界限分明的,因而对象对集合的隶属关係也不是明确的、非此即彼的。这一概念是美国加利福尼亚大学控制论专家L.A.扎德于1965 年首先提出的。模糊集合这一概念的出现使得数学的思维和方法可以用于处理模糊性现象,从而构成了模糊集合论(中国通常称为模糊性数学)的基础。
相等集合
如果两个集合S和T的元素完全相同,则称S与T两个集合相等,记为S=T 。显然有如下关係:
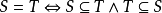
其中符号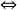 称为若且唯若,表示左边的命题与右边的命题相互蕴含,即两个命题等价。
称为若且唯若,表示左边的命题与右边的命题相互蕴含,即两个命题等价。
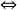
表示方法
表示集合的方法通常有四种,即列举法、描述法、图像法和符号法。
列举法
列举法就是将集合的元素逐一列举出来的方式。例如,光学中的三原色可以用集合{红,绿,蓝}表示;由四个字母a,b,c,d组成的集合A可用A={a,b,c,d}表示,如此等等。
列举法还包括儘管集合的元素无法一一列举,但可以将它们的变化规律表示出来的情况。如正整数集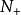 和整数集
和整数集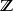 可以分别表示为
可以分别表示为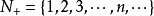 和
和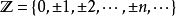 。
。
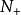
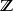
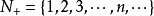
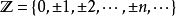
描述法
描述法的形式为{代表元素|满足的性质}。
设集合S是由具有某种性质P的元素全体所构成的,则可以採用描述集合中元素公共属性的方法来表示集合:S={x|P(x)}。例如,由2的平方根组成的集合B可表示为B={x|x2=2}。而有理数集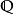 和正实数集
和正实数集 则可以分别表示为
则可以分别表示为 和
和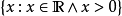 。
。
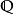


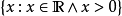
图像法
图像法,又称韦恩图法、韦氏图法,是一种利用二维平面上的点集表示集合的方法。一般用平面上的矩形或圆形表示一个集合,是集合的一种直观的图形表示法,如图2所示。
符号法
有些集合可以用一些特殊符号表示,举例如下: 图2韦恩图集合表示法
图2韦恩图集合表示法
 图2韦恩图集合表示法
图2韦恩图集合表示法N:非负整数集合或自然数集合{0,1,2,3,…}
N*或N+:正整数集合{1,2,3,…}
Z:整数集合{…,-1,0,1,…}
Q:有理数集合
Q+:正有理数集合
Q-:负有理数集合
R:实数集合(包括有理数和无理数)
R+:正实数集合
R-:负实数集合
C:複数集合
∅ :空集(不含有任何元素的集合)
运算定律
交换律:A∩B=B∩A;A∪B=B∪A
结合律:A∪(B∪C)=(A∪B)∪C;A∩(B∩C)=(A∩B)∩C
分配对偶律:A∩(B∪C)=(A∩B)∪(A∩C);A∪(B∩C)=(A∪B)∩(A∪C)
对偶律:(A∪B)^C=A^C∩B^C;(A∩B)^C=A^C∪B^C
同一律:A∪∅=A;A∩U=A
求补律:A∪A'=U;A∩A'=∅
对合律:A''=A
等幂律:A∪A=A;A∩A=A
零一律:A∪U=U;A∩∅=∅
吸收律:A∪(A∩B)=A;A∩(A∪B)=A
反演律(德·摩根律):(A∪B)'=A'∩B';(A∩B)'=A'∪B'。文字表述:1.集合A与集合B的交集的补集等于集合A的补集与集合B的补集的并集; 2.集合A与集合B的并集的补集等于集合A的补集与集合B的补集的交集。
容斥原理(特殊情况):
card(A∪B)=card(A)+card(B)-card(A∩B)
card(A∪B∪C)=card(A)+card(B)+card(C)-card(A∩B)-card(B∩C)-card(C∩A)+card(A∩B∩C)。
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯