读书笔记摘抄新闻资讯
模糊集合
模糊集合是用来表达模糊性概念的集合。 又称模糊集、模糊子集。普通的集合是指具有某种属性的对象的全体。
1965年美国学者扎德在数学上创立了一种描述模糊现象的方法—模糊集合论。这种方法把待考察的对象及反映它的模糊概念作为一定的模糊集合，建立适当的隶属函式，通过模糊集合的有关运算和变换，对模糊对象进行分析。模糊集合论以模糊数学为基础，研究有关非精确的现象。客观世界中，大量存在着许多亦此亦彼的模糊现象。
基本介绍
- 中文名：模糊集合
- 外文名：fuzzy set
- 又名：模糊集、模糊子集
- 提出人物：L.A.扎德
- 提出时间：1965
- 套用学科：数学
定义
这种属性所表达的概念应该是清晰的，界限分明的。因此每个对象对于集合的隶属关係也是明确的，非此即彼。但在人们的思维中还有着许多模糊的概念，例如年轻、很大、暖和、傍晚等，这些概念所描述的对象属性不能简单地用“是”或“否”来回答，模糊集合就是指具有某个模糊概念所描述的属性的对象的全体。由于概念本身不是清晰的、界限分明的，因而对象对集合的隶属关係也不是明确的、非此即彼的。这一概念是美国加利福尼亚大学控制论专家L.A.扎德于 1965 年首先提出的。模糊集合这一概念的出现使得数学的思维和方法可以用于处理模糊性现象，从而构成了模糊集合论（中国通常称为模糊性数学)的基础。
给定一个论域U，那幺从U到单位区间 [0,1] 的一个映射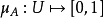
称为U上的一个模糊集，或U的一个模糊子集。
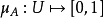
表示
模糊集可以记为A。 映射（函式）μA(·) 或简记为A(·) 叫做模糊集A的隶属函式。 对于每个x∈U，μA(x) 叫做元素x对模糊集A的隶属度。
模糊集的常用表示法有下述几种：
（1）解析法，也即给出隶属函式的具体表达式。
（2）Zadeh 记法，例如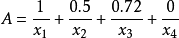
。分母是论域中的元素，分子是该元素对应的隶属度。有时候，若隶属度为0，该项可以忽略不写。
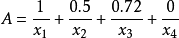
（3）序偶法，例如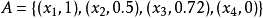
，序偶对的前者是论域中的元素，后者是该元素对应的隶属度。
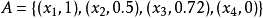
（4）向量法，在有限论域的场合，给论域中元素规定一个表达的顺序，那幺可以将上述序偶法简写为隶属度的向量式，如A= (1,0.5,0.72,0) 。
模糊度
一个模糊集A的模糊度衡量、反映了A的模糊程度，一个直观的定义是这样的：
设映射D:F(U) → [0,1] 满足下述5条性质：
- 清晰性：D(A) = 0 若且唯若A∈P(U)。（经典集的模糊度恆为0。）
- 模糊性：D(A) = 1 若且唯若 ∀u∈U有A(u) = 0.5。（隶属度都为0.5的模糊集最模糊。）
- 单调性：∀u∈U，若A(u) ≤B(u) ≤ 0.5，或者A(u) ≥B(u) ≥ 0.5，则D(A) ≤D(B)。
- 对称性：∀A∈F(U)，有D(A) =D(A)。（补集的模糊度相等。）
- 可加性：D(A∪B) +D(A∩B)=D(A) +D(B)。
则称D是定义在F(U) 上的模糊度函式，而D(A) 为模糊集A的模糊度。
可以证明符合上述定义的模糊度是存在的，一个常用的公式（分别针对有限和无限论域）就是
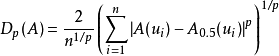
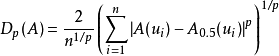
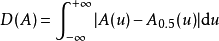
其中p> 0 是参数，称为 Minkowski 模糊度。特别地，当p= 1 的时候称为 Hamming 模糊度或 Kaufmann 模糊指标，当p= 2 的时候称为 Euclid 模糊度。
模糊集的运算
各种运算元
- Zadeh 运算元，max 即为并，min 即为交
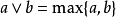
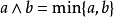
- 代数运算元（机率和、代数积）
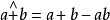
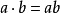
- 有界运算元
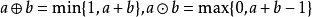
- Einstein 运算元
