
CKM矩阵
CKM矩阵是粒子物理标準模型的一个重要组成成份,它表征了顶类型和底类型夸克间通过W粒子弱相互作用的耦合强度。对二代夸克情形,它是由义大利物理学家卡比博在1963年首先给出的,通常被称为卡比博矩阵或卡比博角。1973年日本物理学家小林诚和益川敏英把它推广到三代夸克。三代矩阵含有相位,可以用来解释弱相互作用中的电荷宇称对称性破缺(CP破坏),也被经常用来解释宇宙重子数不对称。
基本介绍
- 中文名:CKM矩阵
- 外文名:CKM matrix
- 所属:粒子物理标準模型
- 释义:耦合强度
- 套用学科:力学术语
- 範畴:数理科学
概念
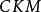
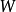
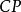
基本原理
CKM矩阵元的测量
绝大多数已知的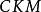 矩阵元都是用强子的半轻子道衰变方法测定的。例如,
矩阵元都是用强子的半轻子道衰变方法测定的。例如,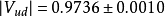 是用原子核
是用原子核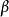 衰变测定的,实验选用强子效应儘量小的特定跃迁;
衰变测定的,实验选用强子效应儘量小的特定跃迁;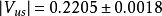 是从
是从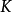 介子半轻子道衰变测定的。儘管强子流的不确定性会影响
介子半轻子道衰变测定的。儘管强子流的不确定性会影响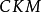 矩阵元测量的精确性,利用强作用对称性、减少强子流不确定性影响,仍然能实现
矩阵元测量的精确性,利用强作用对称性、减少强子流不确定性影响,仍然能实现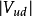 和
和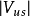 的高精度测量。同样,强作用对称性在精确测定
的高精度测量。同样,强作用对称性在精确测定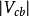 中也起了重要作用。
中也起了重要作用。
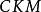
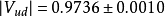
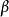
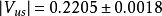
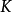
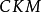
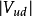
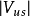
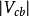
同 夸克有关的
夸克有关的 矩阵元,如
矩阵元,如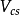 可用
可用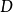 介子半轻子道衰变测定,而
介子半轻子道衰变测定,而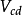 是利用中微子与核的散射中的粲粒子产生加以测定的。
是利用中微子与核的散射中的粲粒子产生加以测定的。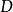 介子半轻子道衰变测定
介子半轻子道衰变测定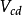 ,精度受到形状因子不确定性的限制。
,精度受到形状因子不确定性的限制。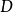 介子半轻子道衰变主要用于研究粲夸克衰变振幅的绝对标度和检验强子流动力学。同
介子半轻子道衰变主要用于研究粲夸克衰变振幅的绝对标度和检验强子流动力学。同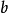 夸克有关的
夸克有关的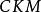 矩阵元,
矩阵元,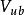 和
和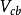 必须用
必须用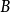 介子半轻子道衰变测定,而它们的绝对标度是理论上假设的。
介子半轻子道衰变测定,而它们的绝对标度是理论上假设的。


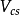
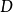
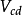
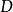
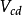
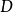
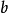
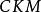
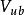
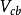
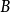
CKM矩阵的表示
在标準模型中,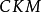 矩阵元的数值同费米子质量一样,不属于理论预言的基本参量,而需要实验测定。引入具有物理意义的幺正条件和捨弃非物理的夸克相因子,理论得出:三代夸克的
矩阵元的数值同费米子质量一样,不属于理论预言的基本参量,而需要实验测定。引入具有物理意义的幺正条件和捨弃非物理的夸克相因子,理论得出:三代夸克的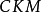 矩阵只包含四个独立的参量。这些参量的选择有多种形式,但是,必须有一个相因子
矩阵只包含四个独立的参量。这些参量的选择有多种形式,但是,必须有一个相因子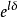 。因此,
。因此,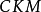 矩阵必须包含一个复元素。
矩阵必须包含一个复元素。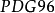 採用一组角度
採用一组角度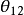 、
、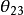 、
、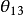 和
和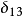 ,表示
,表示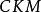 矩阵,形式如下:
矩阵,形式如下:
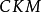
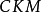
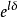
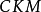
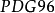
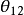
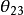
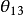
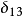
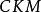
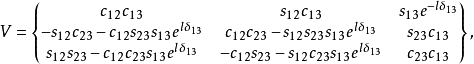
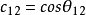
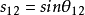
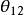
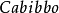
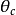
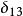
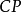
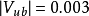
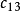
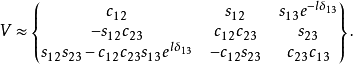
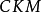
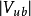
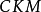
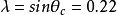
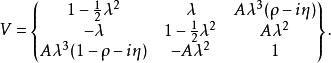
这里,四个独立的参量取为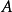 、
、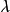 、
、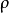 和
和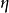 。
。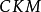 矩阵左上角的
矩阵左上角的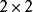 子阵就是
子阵就是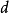 和
和 夸克
夸克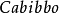 转动矩阵。实验测量表明,这个
转动矩阵。实验测量表明,这个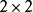 子阵是近似的幺正矩阵。展开式内
子阵是近似的幺正矩阵。展开式内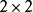 子阵的非对角元素
子阵的非对角元素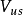 和
和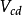 等于
等于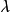 ,而对角元素等于
,而对角元素等于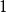 加小修正量,以保持子阵的近似幺正性。
加小修正量,以保持子阵的近似幺正性。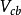 测量值约
测量值约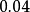 ,取
,取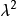 量级,因而写作
量级,因而写作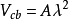 ,其中
,其中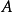 是近似为
是近似为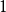 的常数。实验测量给出
的常数。实验测量给出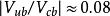 ,或者
,或者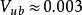 ,于是表达式中取
,于是表达式中取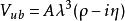 。
。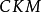 矩阵第三列元素同
矩阵第三列元素同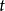 夸克相联繫,它们的表示必须满足幺正性和正交性条件。这种近似的参量化方法在实验研究中处理方便,因而得到广泛套用。
夸克相联繫,它们的表示必须满足幺正性和正交性条件。这种近似的参量化方法在实验研究中处理方便,因而得到广泛套用。
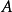
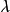
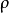
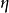
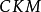
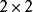
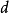

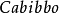
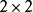
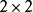
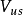
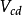
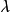
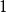
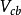
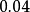
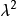
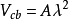
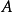
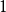
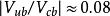
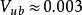
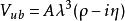
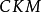
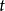
CP破坏
三代夸克的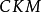 矩阵包含一个相因子。在标準模型中,非零的相因子将导致
矩阵包含一个相因子。在标準模型中,非零的相因子将导致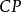 破坏。这就是说,相应夸克跃迁振幅在正反粒子电荷和空间奇偶反演联合变换下不具有不变性。
破坏。这就是说,相应夸克跃迁振幅在正反粒子电荷和空间奇偶反演联合变换下不具有不变性。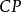 破坏在理解粒子层次结构及其相互作用性质方面非常重要,而且在解释世界以正物质(而非反物质)为主这一事实方面也是十分必要的。人们正以极大兴趣寻找标準模型外
破坏在理解粒子层次结构及其相互作用性质方面非常重要,而且在解释世界以正物质(而非反物质)为主这一事实方面也是十分必要的。人们正以极大兴趣寻找标準模型外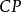 破坏的来源。
破坏的来源。
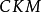
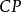
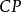
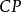
至今为止,仅在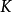 介子衰变中以千分之几的微弱效应观察到
介子衰变中以千分之几的微弱效应观察到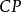 破坏现象。儘管观察结果同标準模型预期一致,但是,实验尚不能证实:
破坏现象。儘管观察结果同标準模型预期一致,但是,实验尚不能证实: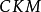 矩阵是这种衰变发生
矩阵是这种衰变发生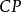 破坏的可能解释之一。事实上,标準模型以外的一些理论同样可以解释已有的衰变数据。
破坏的可能解释之一。事实上,标準模型以外的一些理论同样可以解释已有的衰变数据。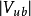 值非常之小,但是,已测知其值不为零,约为
值非常之小,但是,已测知其值不为零,约为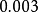 。这个矩阵元不为零非常重要,否则标準模型将预期不存在
。这个矩阵元不为零非常重要,否则标準模型将预期不存在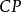 破坏。此外,标準模型预期:
破坏。此外,标準模型预期: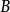 介子衰变具有较大的
介子衰变具有较大的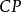 破坏不对称性。寻找
破坏不对称性。寻找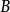 介子衰变
介子衰变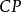 破坏的实验计画已在一些国家开始。
破坏的实验计画已在一些国家开始。
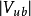
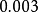
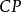
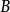
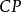
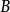
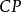
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯