
.极限集
极限集(limit set)是动力系统由极限点组成的集合。极限点指随着时间向正负两个方向趋于无穷时该点所在的轨道会无穷次接近它的点。如果只考虑时间趋于正或负无穷,则可分别得到ω极限集或α极限集。极限集是动力系统研究的基本对象。轨道的极限集是不变闭集,如果相空间是紧的,极限集也总存在。不动点和周期轨都是极限集的例子。根据庞卡莱-班狄克逊(Poincaré-Bendixson)定理,平面向量场的极限集通常由有限条轨道与平衡点连线而成。空间系统的极限集有时很複杂,如奇怪吸引子。
基本介绍
- 中文名:极限集
- 外文名:limit set
- 所属领域:动力系统
- 分类:ω极限集或α极限集
- 性质:动力系统研究的基本对象
定义
如果存在趋∞于的时间序列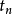 使得
使得 收敛于
收敛于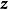 ,则称
,则称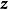 是轨线
是轨线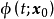 或点
或点 的
的 极限点。这表明当
极限点。这表明当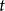 趋向于
趋向于 时,
时,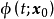 无数次地靠近
无数次地靠近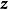 ,
, 所有
所有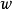 极限点的集合称为是
极限点的集合称为是 极限集,记作
极限集,记作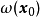 。
。
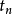

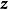
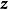
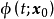


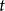

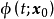
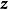

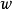

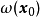
类似地,如果存在趋于 的时间序列
的时间序列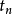 使得
使得 收敛于
收敛于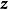 ,则称
,则称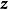 是轨线
是轨线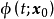 或点
或点 的
的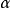 极限点,
极限点, 所有
所有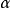 极限点的集合称为
极限点的集合称为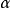 极限集,记作
极限集,记作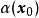 。
。

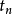

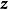
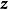
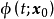

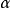

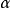
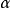
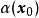
相关性质定理
设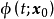 是一条轨线,则下面
是一条轨线,则下面 极限集的性质成立:
极限集的性质成立:
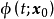

(i) 极限集只依赖于轨线而不依赖于特定点, 因此对任意的t,有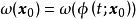 ;
;
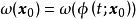
(ii) 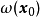 是不变集:若
是不变集:若 ,那幺对所有的正t或负t,轨线
,那幺对所有的正t或负t,轨线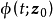 都属于
都属于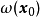 ;
;
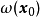

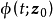
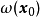
(iii) 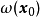 是闭集(即
是闭集(即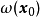 包含它所有的极限点);
包含它所有的极限点);
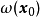
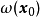
(iv) 若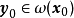 , 则有
, 则有 ;
;
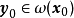

另外,若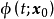 对
对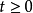 是有界的(即存在常数C使得
是有界的(即存在常数C使得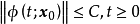 ,则下面的(v)和(vi)也成立:
,则下面的(v)和(vi)也成立:
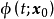
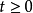
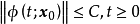
(v) 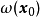 非空;
非空;
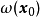
(vi) 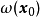 是连通的,即它不能由多块区域组成。
是连通的,即它不能由多块区域组成。
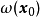
若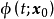 对
对 是有界的,则
是有界的,则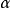 极限集有类似的性质。
极限集有类似的性质。
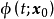

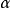
性质(i)可直接由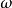 极限集的定义推出。
极限集的定义推出。
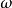
性质(ii)可由流的连续性得到。
若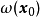 中的序列
中的序列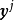 收敛于
收敛于 ,而
,而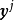 是
是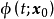 的极限点,这两点相结合可推出性质(iii)。
的极限点,这两点相结合可推出性质(iii)。
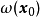
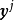

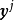
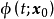
由性质(ii)和(iii)可推出性质(iv)。
性质(v)成立是因为轨线要不断地回到相空间中的某处。
性质(vi)成立是因为轨线本身是连通的。

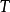
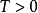
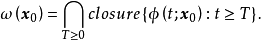
例题分析
例1 考虑方程组

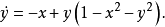
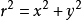
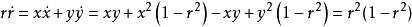
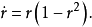
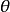
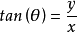
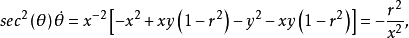
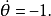
因此,解沿逆时针方向、以相同的角速度绕原点旋转,关于r的方程有一个吸引的不动点r=1和一个排斥的不动点r=0.从而在平面坐标下的方程有一个半径为1的圆形周期轨道,和一个排斥的不动点——原点,参见图1(a)
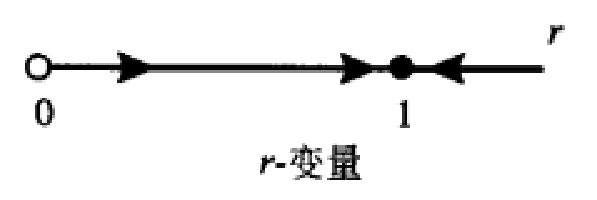 图1(a)
图1(a)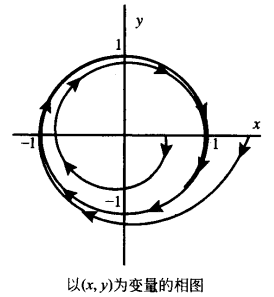 图1(b)
图1(b)从单位圆外出发的轨线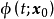 都趋向于该单位圆,而不是趋于圆上的某个点,但对于圆上任一点z,
都趋向于该单位圆,而不是趋于圆上的某个点,但对于圆上任一点z,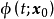 每经过
每经过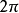 单位的时间后更接近于z,因此存在时间序列
单位的时间后更接近于z,因此存在时间序列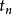 使得
使得 收敛于z.显然所取的z不同得到的
收敛于z.显然所取的z不同得到的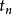 也不同,鑒于只考虑t趋向于无穷的情况,所有这些点所成之集称为
也不同,鑒于只考虑t趋向于无穷的情况,所有这些点所成之集称为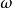 极限集,这种记法考虑到了
极限集,这种记法考虑到了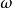 是希腊字母表的最后一个字母。同理,t趋向负无穷时轨线的极限点集称为是
是希腊字母表的最后一个字母。同理,t趋向负无穷时轨线的极限点集称为是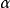 极限集。
极限集。
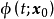
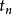

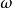
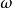
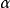
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯