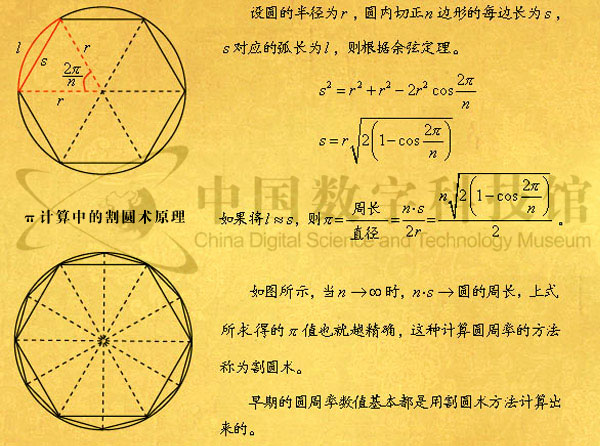
极限理论
极限理论是研究关于极限的严格定义、基本性质和判别準则等问题的基础理论。
极限思想的萌芽可以追溯到古希腊时期和中国战国时期,但极限概念真正意义上的首次出现于沃利斯的《无穷算数》中,牛顿在其《自然哲学的数学原理》一书中明确使用了极限这个词并作了阐述。但迟至18世纪下半叶,达朗贝尔等人才认识到,把微积分建立在极限概念的基础之上,微积分才是完善的,柯西最先给出了极限的描述性定义,之后,魏尔斯特拉斯给出了极限的严格定义(ε-δ和ε-N定义)。
从此,各种极限问题才有了切实可行的判别準则,使极限理论成为了微积分的工具和基础。
基本介绍
- 中文名:极限理论
- 外文名:Theory of limit
- 别名:极限论
- 所属学科:数学
- 理论基础:实数理论
- 研究内容:极限的定义、基本性质、判别準则
极限定义
数列极限
定义:设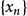 为一无穷数列,如果存在常数
为一无穷数列,如果存在常数 ,对于任意给定的正数
,对于任意给定的正数 (不论它多幺小),总存在正整数
(不论它多幺小),总存在正整数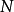 ,使得当
,使得当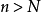 时的一切
时的一切 ,均有不等式
,均有不等式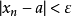 成立,那幺就称常数
成立,那幺就称常数 是数列
是数列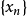 的极限,或称数列
的极限,或称数列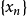 收敛于
收敛于 。
。 数列极限
数列极限


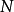
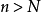

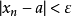

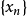
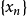

 数列极限
数列极限记为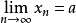 或
或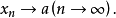
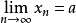
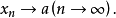
用逻辑符号可以表示为:
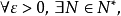
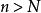
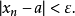
或者: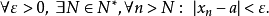
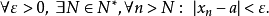
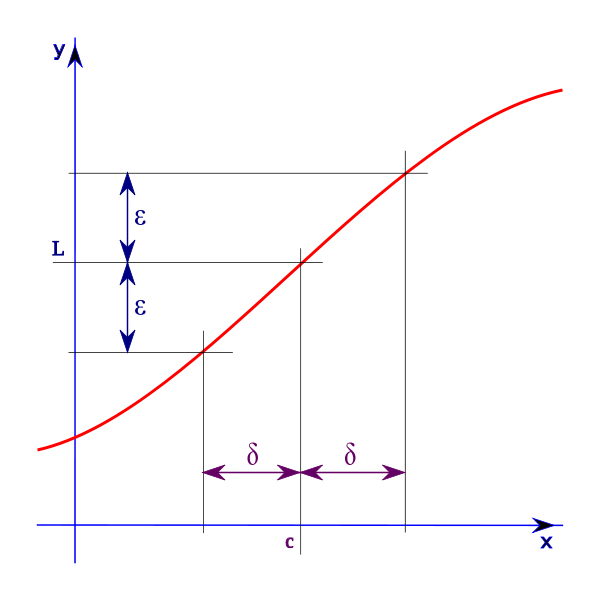
函式极限
定义:设函式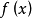 在点
在点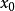 的某一去心邻域内有定义,如果存在常数
的某一去心邻域内有定义,如果存在常数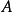 ,对于任意给定的正数
,对于任意给定的正数 (无论它多幺小),总存在正数
(无论它多幺小),总存在正数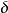 ,使得当
,使得当 满足不等式
满足不等式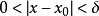 时,对应的函式值
时,对应的函式值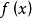 满足不等式
满足不等式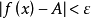 ,那幺常数
,那幺常数 就叫做函式
就叫做函式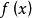 当
当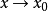 时的极限,或称函式
时的极限,或称函式 收敛于
收敛于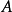 .
. 函式极限
函式极限
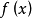
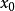
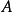

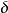

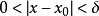
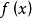
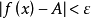

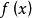
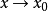

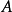
 函式极限
函式极限记为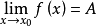 或
或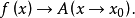
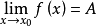
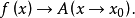
用逻辑符号可以表示为:
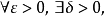
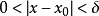
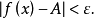
或者: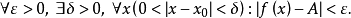
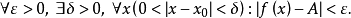
历史背景
微积分一诞生,就在力学、天文学中大显身手,能够轻而易举地解决许多本来认为束手无策的难题。后来,微积分又在更多的领域取得了丰硕的成果。人们公认微积分是17、18世纪数学所达到的最高成就,然而它的创始人牛顿和莱布尼茨对之所作的论证却并不清楚、很不严谨。无论是牛顿的瞬和流数,还是莱布尼茨的dx和,都涉及到"无穷小量",而在他们各自的论述中都没有给出确定的、一贯的定义。在微积分的推导和运算过程中,常常是先用无穷小量作为分母进行除法,然后又把无穷小量当作零,以消除那些包含有它的项。那幺"无穷小量"究竟是零还是非零呢?如果它是零,怎幺能用它去作除数呢?如果它不是零,又怎幺能把包含它的那些项消除掉呢?这种逻辑上的矛盾,牛顿和莱布尼茨都意识到了。牛顿曾用有限差值的最初比和最终比来说明流数的意义,但是当差值还未达到零时,其比值不是最终的,而当差值达到零时,它们的比就成为,怎样理解这样的最终比呢?实在令人困惑。牛顿承认他对自己的方法只作出"简略的说明,而不是正确的论证。"莱布尼茨曾把无穷小量形容为一种"理想的量",但正如一些数学家所说:"与其说是一种说明,还不如说是一个谜。" 牛顿
牛顿 贝克莱
贝克莱
 牛顿
牛顿 贝克莱
贝克莱奇怪的是,微积分自身存在着明显的逻辑混乱,然而在实际套用中则是卓有成效的得力工具。这样,微积分就具有了"神秘性"。起初,"神秘性"集中表现在对于"无穷小量"这个概念的理解上,并因而受到了各种人的攻击。数学家们不能容忍这一新方法的理论本身是如此的含糊不清乃至荒谬绝伦。法国数学家洛尔称微积分为"巧妙的谬论的汇集";着名思想家伏尔泰说微积分是"精确的计算和度量某种无从想像其存在的东西的艺术"。在一片疑难和责问声中,以英国主教兼哲学家贝克莱的谴责最为强烈,他讥讽无穷小量是"逝去的量的鬼魂",说微积分包含"大量的空虚、黑暗和混乱",是"分明的诡辩"。
马克思曾对微积分作过一番历史考察,他把这一时期称为"神秘的微积分"时期,并有这样的评论:"于是,人们自己相信了新发现的算法的神秘性。这种算法肯定是通过不正确的数学途径得出了正确的(而且在几何套用上是惊人的)结果。人们就这样把自己神秘化了,对这新发现的评价更高了,使一群旧式正统派数学家更加恼怒,并且激起了敌对的叫嚣,这种叫嚣甚至在数学界以外产生了反响,而为新事物开拓道路,这是必然的。" 达朗贝尔
达朗贝尔
 达朗贝尔
达朗贝尔微积分的逻辑缺陷和人们的猛烈攻击,激厉数学家们为消除微积分的神秘性,亦即为微积分建立合理的理论基础而努力。18世纪,在这方面作出贡献的主要代表人物是达朗贝尔、欧拉和拉格朗日。可是"无穷小量"的本质尚未弄明白,无穷级数的"和"的问题又日渐突出了。在微积分里,一个典型的基本算法就是把无穷多项相加,叫做求无穷级数之和。在初等数学中,有限多项相加总有确定的和。而无穷多项相加,是加不完的,什幺是无穷级数的"和"是不清楚的。在很长一段时间里,人们习惯地把有限多项相加的运算规则照搬到无穷级数中,虽然也解决过许多问题,但有时竟出现了像1/2=0这样的荒谬结果。
进入19世纪以后,随着微积分套用的更加广泛和深入,遇到的数量关係也更加複杂,很多问题,例如,对于热传导现象的研究,就已超出了早年力学那样的直观性。在这种情况下,要求有明确的概念、合乎逻辑的推理和运算法则,就显得更加重要和迫切了。事实上,微积分作为变数数学,是运用"无穷"来描画和研究运动和变化过程,获得了成功的,却长期没有对有关"无穷"的概念给出正确的阐述,甚至导致逻辑上的混乱,微积分的神秘性正是由此而来,而这也正是微积分的理论基础所要解决的问题。 柯西
柯西
 柯西
柯西数学家们经过一百多年的艰苦探索历程,终于在前人所积累的大量成果(包括许多失败的尝试)的基础上,建立起微积分的理论基础。柯西(1789―1857)于1821年出版的《分析教程》中,开始有了极限概念的基本明确的叙述,并以极限概念为基础,对"无穷小量"、无穷级数的"和"等概念给出了比较明确的定义。例如,从极限的观点看,"无穷小量"就是极限为零的变数,在变化过程中,它可以是"非零",但它的变化趋向是"零",无限地接近于"零"。极限论正是从变化趋向上说明了"无穷小量"与"零"的内在联繫,从而澄清了逻辑上的混乱,撕下了早期微积分的神秘面纱。后来,经过波尔察诺、魏尔斯特拉斯、戴德金、康托等人的卓越工作,又进一步把极限论建立在严格的实数理论基础上,并且形成了描述极限过程的ε-δ语言。微积分理论基础的严密化,使微积分跃进和扩展为现代数学的重要领域。
微积分的发展历史告诉我们,一门学科不能只停留在感性阶段,如果不上升到理性,不具备坚实的理论基础,不但其套用受到限制,学科本身也难以继续发展。然而在上一世纪我国的多次运动中,在"数学是唯心主义的世袭领地"这种错误思想影响下,极限论和ε-δ语言屡遭批判,屡次被撵出课堂。"文革"之后,一位教师感慨地说:"当我做学生的时候,也曾起劲地参加批判,但毕业以后,做了几年教学工作,我体会到过去批判的东西其实是正确的、有重要意义的。可是当我向学生讲述这些道理的时候,我自己却又成为学生们的批判对象了。" 魏尔斯特拉斯
魏尔斯特拉斯
 魏尔斯特拉斯
魏尔斯特拉斯恩格斯早就指出:"一个民族想要站在科学的最高峰,就一刻也不能没有理论思维。"
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯