读书笔记摘抄新闻资讯费希尔信息
费希尔信息（Fisher Information）（有时简称为信息[1]）是一种测量可观察随机变数X携带的关于模型X的分布的未知参数θ的信息量的方法。形式上，它是方差得分，或观察到的信息的预期值。在贝叶斯统计中，后验模式的渐近分布取决于Fisher信息，而不依赖于先验（根据Bernstein-von Mises定理，Laplace为指数族预测）。[2]统计学家Ronald Fisher强调了Fisher信息在最大似然估计渐近理论中的作用（遵循Francis Ysidro Edgeworth的一些初步结果）。 Fisher信息也用于Jeffreys先验的计算，用于贝叶斯统计。Fisher信息矩阵用于计算与最大似然估计相关联的协方差矩阵。它也可以用于测试统计的制定，例如Wald测试。
基本介绍
- 中文名：费希尔信息
- 外文名：Fisher Information
定义
品质函式的方差称为费希尔信息，用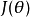
表示，定义为：
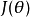
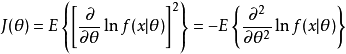
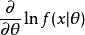
介绍
Fisher信息是一种测量可观察随机变数X携带的关于X的机率所依赖的未知参数θ的信息量的方式。 令f（X;θ）为X的机率密度函式（或机率质量函式），条件是θ的值。 这也是θ的似然函式。 它描述了在给定已知的θ值的情况下观察给定样本X的机率。 如果f相对于θ的变化急剧地达到峰值，则很容易从数据中指示θ的“正确”值，或者等效地，数据X提供关于参数θ的大量信息。 如果似然f是平坦的并且展开，则需要许多很多样本（如X）来估计使用整个採样群体获得的θ的实际“真实”值。 这表明研究了关于θ的某种方差。
套用
实验的最佳化设计
Fisher信息广泛用于最佳实验设计。由于估计器 - 方差和Fisher信息的互易性，最小化方差对应于最大化信息。
当线性（或线性化）统计模型具有多个参数时，参数估计器的均值是向量，其方差是矩阵。方差矩阵的逆被称为“信息矩阵”。因为参数矢量的估计量的方差是矩阵，所以“最小化方差”的问题是複杂的。统计学家使用统计理论，使用实值汇总统计数据压缩信息矩阵;作为实值函式，这些“信息标準”可以最大化。
传统上，统计学家通过考虑协方差矩阵（无偏估计量）的一些汇总统计量来评估估计量和设计，通常具有正实数值（如行列式或矩阵迹线）。使用正实数带来了几个优点：如果单个参数的估计具有正方差，则方差和Fisher信息都是正实数;因此它们是非负实数的凸锥的成员（其非零成员在同一个锥体中具有倒数）。对于几个参数，协方差矩阵和信息矩阵是在Loewner（Löwner）阶下在部分有序向量空间中非负定对称矩阵的凸锥的元素。该锥体在矩阵加法和反演下以及在正实数和矩阵的乘法下闭合。 Pukelsheim出现了矩阵理论和Loewner秩序的论述。
传统的最优性标準是信息矩阵的不变数，在不变数理论意义上;在代数上，传统的最优性标準是（Fisher）信息矩阵的特徵值的函式（参见最优设计）。
杰弗里斯先前在贝叶斯统计中
在贝叶斯统计中，Fisher信息用于计算Jeffreys先验，这是连续分布参数的标準无信息先验。
计算神经科学
Fisher信息已被用于发现神经代码準确性的界限。在那种情况下，X通常是表示低维变数θ（例如刺激参数）的许多神经元的联合回响。特别是研究了相关性在神经反应噪声中的作用。
物理定律的推导
费舍尔信息在弗里登提出的有争议的原则中起着核心作用，该原则是物理定律的基础，这一主张一直存在争议。
机器学习
Fisher信息用于机器学习技术，如弹性权重合併，它可以减少人工神经网路中的灾难性遗忘。