
费希尔不等式
费希尔不等式(Fisher's inequality)是反映设计存在的一种条件,指(v,b,r,k,λ)-BIBD存在时,参数b与v必须满足的不等式:b≥v,该不等式由费希尔(R.A.Fisher)于1940年发现,后来雷·乔德里(D.K.Ray-Chaudhuri)和威尔森(R.M.Wilson)将这个不等式推广到t设计的情形。
基本介绍
- 中文名:费希尔不等式
- 外文名:Fisher's inequality
- 所属学科:数学(组合学)
- 简介:反映设计存在的一种条件
基本介绍
费希尔不等式在(b,v,r,k,λ)设计中,b≥v。
雷·乔德里(D.K.Ray-Chaudhuri)和威尔森(R.M.Wilson)将这个不等式推广到t设计的情形。他们证明:若2s-(v,k,λ)设计存在,且v≥k+s,则

若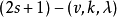 设计存在,且
设计存在,且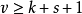 ,则
,则
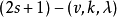
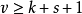
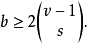
费希尔不等式的证明
为了证明这一结果,需要引入一个很有帮助的概念,这就是区组设计的关联矩阵(incidence matrix),如果一个设计有变元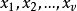 ,区组
,区组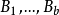 ,那幺A是一个由0和1组成的v×b矩阵,其中,如果xi在Bj中则A的i,j项是1,否则它是0(这就是点集关联矩阵)。
,那幺A是一个由0和1组成的v×b矩阵,其中,如果xi在Bj中则A的i,j项是1,否则它是0(这就是点集关联矩阵)。
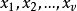
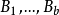
为了证明费希尔不等式,我们先给出以下结果,其证明请参考相应文献。
定理1 在一个(b,v, r, k,λ)设计中有
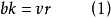
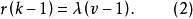
定理2如果A是(b,v, r, k,λ)设计的关联矩阵,那幺
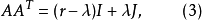
费希尔不等式的证明:
我们假设b<v,并推导出一个矛盾。设A是关联矩阵。
因为b<v,所以我们可以把v-b个0列加到A上,结果给出一个v×v方阵B,现在AAT= BBT,因为A的两行的内积等于B的两行的内积。取行列式,我们得出下面的结论:
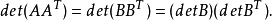
但是,detB=0,因为B有0列。因此,det(AAT)=0。现在,根据定理2,有



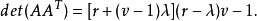
因为我们已得出结论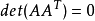 ,所以我们有
,所以我们有
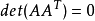

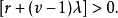
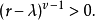
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯