读书笔记摘抄新闻资讯
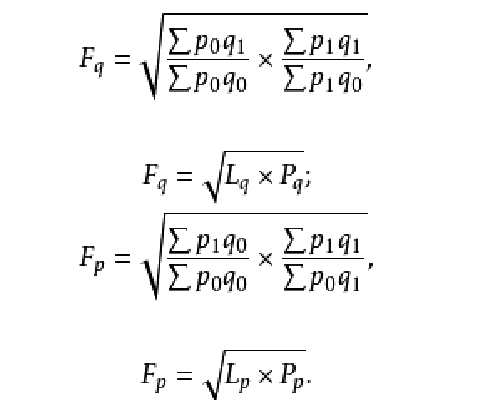
费舍理想指数
Fisher理想指数(Fisher's ideal indices)也叫费希尔理想指数、费舍理想指数等，它包括价格指数和物量指数。费希尔理想价格指数是拉氏价格指数和帕氏价格指数的几何平均值，即：Fp=(Lp·Pp)；费希尔理想物量指数是拉氏物量指数和帕氏物量指数的几何平均值，即：Fq=(Lq·Pq)费希尔将这两个指数称为“理想”指数是因为它们符合他认为重要的各种检验，例如“时间转换”和“因子转换”检验。时间转换检验要求以时期0为基础的时期t的指数应是以时期t为基础的时期0的指数的倒数。因子转换检验要求价格指数和物量指数的乘积应等于现值的对称变化ΣVt/ΣV0。拉氏指数和帕氏指数本身通不过这两种检验。因此，费希尔指数有很大的吸引力，在经济统计中被广泛使用。
基本介绍
- 中文名：费舍理想指数
- 外文名：Fisher's ideal indices
- 所属学科：数学（统计学）
- 别名：Fisher理想指数、费希尔理想指数
- 提出者：统计学家Fisher
- 提出时间：1922
- 相关概念：拉氏指数、帕氏指数等
- 套用学科：经济统计
基本介绍
理想指数(Idealindex)美国的统计学家Fisher(翻译为费舍、费雪、费希尔、费休等)于1922年提出的，它是基期加权综合指数(即拉氏指数) 与现期加权综合指数(即帕氏指数)加以几何平均得出的一种指数。有两种形式：理想物量指数和理想价格指数，公式如下：
Fisher理想指数的优缺点
优点
Fisher理想指数有着许多令人满意的统计和经济理论上的性质，能够满足些重要的统计检验，如时间转换检验和因子转换检验等(而拉氏指数和派氏指数本身都不能通过这些检验)。同时由于Fisher理想指数体系融综合指数的两套分析体系于一体，兼顾并中和了拉氏指数和派氏指数由于权数选择不同而导致的差异性，从而避免了综合指数的失真性。正是由于Fisher指数所具有的良好性质，它在经济统计中被广泛套用，有着很大的吸引力。
缺点
儘管Fisher 指数是“理想的”，但它仍然存在一些不足之处：首先，Fisher指数要求它的数据达到能计算拉氏指数和派氏指数的要求，数据需求量大。这不仅会增加核算费用，而且会由于工作量的加大而导致计算和结果公布的延迟。其次，Fisher指数不像拉氏指数和派氏指数那样容易理解。拉氏指数和派氏指数可以简单地解释为计量指定的一揽子货物和服务的价值变化，而Fisher指数不可以。再次，Fisher指数不具有可加一致性，即使对于最基本的年度间数据变化也是如此。这一缺陷严重製约了它在核算框架中的套用。