
空间分析算法
空间分析(Spatial Analysis,SA)是地理信息系统(GIS)的核心功能,它通过研究地理空间数据及其相应分析理论、方法和技术,探索、证明地理要素之间的关係,揭示地理特徵和过程的内在规律和机理,实现对地理空间信息的认知、解释,预测和调控。空间分析算法有平面扫描算法、空间拓扑分析算法、凸包的算法、Voronoi图算法和最短路径算法等。
基本介绍
- 中文名:空间分析算法
- 外文名:Spatial Analysis Algorithm
- 相关概念:地理信息系统
- 套用:等水污染监测、城市规划与管理
- 分类:矢量数据、栅格数据空间分析
- 主要算法:平面扫描算法、凸包的算法等
背景
地理信息系统(Geographic Information System,简称GIS)是採集、处理、存储、查询、分析和显示与地球表面空间相关的数据的计算机系统。对于具体套用来说,它是利用计算机科学管理和综合分析现实世界与空间位置相关的地理数据,为规划、管理、研究等提供辅助决策的信息系统。
空间分析是建立在对空间数据的有效管理之上的,是地理信息系统区别于一般信息系统的主要功能特徵,也成为评价一个空间信息系统功能的主要指标之一。空间分析是基于空间对象的位置和形态特徵的空间数据分析技术,其目的在于提取和传输空间信息。利用空间分析技术,通过对原始数据模型的观察和实验,用户可以获得新的经验和知识,并以此作为空间行为的决策依据。空间分析在水污染监测、城市规划与管理、地震灾害和损失估计、洪水灾害分析、矿产资源评价、道路交通管理、地形地貌分析和军事领域等领域都有广泛套用。
平面扫描算法
平面扫描算法的主要内容是对空间对象进行一遍扫描,并在扫描过程中完成对空间对象的性质或空间对象之间的关係的分析。在扫描过程中,扫描线自左向右移动,依一定顺序遍历所有与扫描线相交的空间元素,判断它们之间的顺序和其他空间拓扑关係,依照一定规则进行分析。图 1 中给出了平面扫描算法的示意,其中粗线段表示和扫描线相交的线段。
任何平面扫描算法的基本要素都包括:事件点列表,扫描线状态,事件点触发的动作。 其中,事件点列表 指依照系统确定的空间排序关係,事先确定或在扫描过程中计算出的算法感兴趣的空间元素的有序序列;扫描线状态指依照确定的排序规则记录当前与扫描线相交的空间元素的有序表 ;事件点触发的动作指扫描到事件点时做出的分析或操作。
事先确定的事件点列表在扫描过程中不再变化,称为静态事件点列表;需要在扫描过程中计算的事件点列表称为动态事件点列表。和扫描线相交的线段以及落在扫描线上的点是扫描线状态的组成元素。事件点可以是任何分析算法感兴趣的空间元素,包括对象之间交点和特定线段元素等。
可以将扫描线状态看成一种抽象数据类型,记为 Sweep_Status,它拥有自己的数据组织方式、排序规则和操作方法。扫描线状态中的排序规则是按照各个空间元素和扫描线交点的 Y 坐标的大小来排序,在这种排序关係的组织下可以对一个与扫描线相交的空间元素取前驱或则后继。图 1 中标号 1 到 4 给出了与扫描线相交的线段的排序顺序。
平面扫描算法是一个算法框架,给定上述三个要素的具体实现,就可以给定一个具有一定的功能的空间分析算法。下面 S 是 Sweep_Status 类型的变数,s 是空间线段,对扫描线状态定义一系列操作。
关于扫描线状态的操作:
(1) new_sweep(),生成一个新的扫描线状态的数据结构,返回 Sweep_Status类型的变数;
(2) add_left(S,s),当扫描过程中遇到左半线段类型的事件点的时候,向 S 中插入一个左半线段对应的线段元素 s,操作返回一个插入线段后的扫描线状态;
(3) del_right(S,s),当扫描过程中遇到右半线段类型的事件点的时候,在扫描线中删除右半线段对应的线段元素, S、s 及返回值的定义同 add_left(S,s);
(4) pred_of(S,elem),在扫描线状态中定位空间元素 elem 的前驱,即确定存在于S中且按照扫描线的排序规则比elem小的元素的集合中最大的元素的位置,操作结果设定 S 的数据项 current 指向 elem 的前驱,current = 0 表示前驱不存在,返回 current 被设定后的扫描线状态;
(5) current_exists(S),当 S 的数据项 current = 0,返回 FALSE,否则返回 TRUE;
(6) set_attr(S,attr)设定 S 中 current 所指的空间元素的属性,attr 是属性集合;
(7) get_attr(S)取 S 中 current 所指的空间元素的属性,返回属性集合;
InsideAbove 是区域类型对象 R 中的线段的一个属性,它表示这个线段的上方或者左侧是区域的内部。可以用平面扫描算法判断并设定 R 中的线段 s 是否具有属性 InsideAbove:如果它在扫描线状态中的序号为奇数,则 s 具有属性InsideAbove;否则不具备这种属性。这种判断和设定在建立空间对象的时候完成,图1中给出了示例。
凸包的算法
平麵点集 S 的凸包是包含 S 中所有点的最小凸多边形,其顶点为 S 中的点。
设多边形 Q 的顶点是给定平面内的点 ,如果线段
,如果线段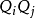 (i ≠ j,1 ≤ i ≤ n,1 ≤ j ≤ n)总不在多边形 Q 外,则称 Q 为凸多边形。
(i ≠ j,1 ≤ i ≤ n,1 ≤ j ≤ n)总不在多边形 Q 外,则称 Q 为凸多边形。

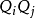
设二维点集 S = {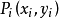 │1 ≤ i ≤ n, 1 ≤ j ≤ n, |s| = n}由给定平面内的点构成。如果凸多边形 Q 的任意顶点
│1 ≤ i ≤ n, 1 ≤ j ≤ n, |s| = n}由给定平面内的点构成。如果凸多边形 Q 的任意顶点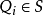 ,且 Q 是可覆盖 S 中各点的最小凸多边形,则称凸多边形 Q 为二维点集 S 的凸包。
,且 Q 是可覆盖 S 中各点的最小凸多边形,则称凸多边形 Q 为二维点集 S 的凸包。
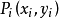
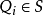
许多空间分析问题都可以归结为凸包问题,求取凸包的算法有增量法、格雷厄姆扫描法、卷包裹法和分治法等。
(1) 增量法:首先取几个点,形成初始凸包,然后不断寻找当前凸包外的新顶点来更新凸包,直到所有的点都在凸包内。其计算複杂度为 O(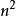 )。
)。
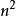
(2) 格雷厄姆扫描法:首先找到最小 Y 坐标点,接着按照其它点和该极值点的连线与 x 轴的夹角的角度值排序,通过判断连续 3 个点的空间关係,从而得到逆时针排列的凸包顶点。其计算複杂度为 O(nlogn)。
(3) 卷包裹法:以某极值点作为开始点,根据其他点都位于相邻顶点连线同侧的原则,找到所有的顶点。其计算複杂度为 O(nh),这里 n 和 h 分别为点数和凸包边界数。
(4) 分治法:先按坐标将点集分成 2 个子集 L 和 R,使得 L 中所有的点在 R的左边,递归地找到 L 和 R 的凸包,通过子凸包的公切线对其合併。其计算複杂度为 O(nlogn)。
所有这些算法的计算複杂度都大于或等于 O(nlogn),凸包算法时间複杂度的下限为 O(nlogn),虽然有些算法在特殊情况下可以达到线性时间的複杂度,不过在最坏的情况下,计算複杂度仍不低于 O(nlogn)。
最短路径算法
由图论的知识可知,地图上的点构成一带权无向图(有向图可视为特例的一种),要找出任意两地间的最短路径,对地图中的所有点,首先要建立一个邻接矩阵,它表示图中任意两地间的邻接关係及其权值(若两地间无任何连线关係则设为无穷大),易知该矩阵为对称矩阵。从该矩阵出发,可以利用图论中的迪杰斯特拉(Dijkstra)算法、弗洛伊德(Floyd)算法等求出最短路径。
Dijkstra算法
Dijkstra算法的基本思路是:首先,引进一个辅助向量Dist,它的每个分量Dist [i]表示当前找到的从始点V到每个终点Vi 的最短路径的长度。它的初始值为:若从V到Vi有弧,则Dist [i]为弧上的权值;否则置Dist[i]为无穷大。显然,长度为Dist[i]=Min{Dist[i]|Vi V}的路径就是从V出发的长度最短的一条路径。此路径为(V, V j )。一般情况下,假设S为已求得最短路径的终点的集合,则可证明:下一条最短路径(设其终点为X)或者是弧(V, X),或者是中间只经过S中的顶点而最后到达顶点X的路径。因此,下一条长度次短的最短路径的长度为:Dist[i]=Min{Dist[i]|Vi
V}的路径就是从V出发的长度最短的一条路径。此路径为(V, V j )。一般情况下,假设S为已求得最短路径的终点的集合,则可证明:下一条最短路径(设其终点为X)或者是弧(V, X),或者是中间只经过S中的顶点而最后到达顶点X的路径。因此,下一条长度次短的最短路径的长度为:Dist[i]=Min{Dist[i]|Vi S},其中Dist[i]或者是弧(V, Vi)上权值,或者是Dist[k] (Vk
S},其中Dist[i]或者是弧(V, Vi)上权值,或者是Dist[k] (Vk S)和弧(Vk, Vi)上的权值之和。
S)和弧(Vk, Vi)上的权值之和。



Dijkstra算法描述为:
(1) 假设用带权的邻接矩阵Cost来表示带权有向图,Cost[i,j]表示弧(Vi , V j)上权值。若(Vi,Vj)不存在,则置Cost[i,j]为无穷大。S为已找到从V出发的最短路径的终点的集合,它的初始状态为空集。
(2) 选择Vj,使得Dist [i] =Min {Dist [i] |Vi 不 S, Vi
S, Vi  V} , Vj就是当前求得的一条从V出发的最短路径的终点。令S=S U { j}(标记j)。(3) 修改从出发到集合V-S上所有顶点Vk可达的最短路径长度。如果Dist[j]+Cost[j, k]<Dist[k]则修改Dist [k]为:(也称为鬆弛操作)Dist[k]=Dist[j]+Cost[j,k]。
V} , Vj就是当前求得的一条从V出发的最短路径的终点。令S=S U { j}(标记j)。(3) 修改从出发到集合V-S上所有顶点Vk可达的最短路径长度。如果Dist[j]+Cost[j, k]<Dist[k]则修改Dist [k]为:(也称为鬆弛操作)Dist[k]=Dist[j]+Cost[j,k]。


(4) 重複操作(2) , (3)共N-1次。由此求得从V到图上其余各顶点的最短路径是依路径长度递增的序列。
弗洛伊德算法
弗洛伊德算法能够求得每一对顶点之间的最短路径,其基本思想是:假设从顶点Vi到Vj的最短路径。若从Vi到Vj有弧,则从Vi到Vj存在一条长度为COST [ i, j]的路径,该路径不一定是最短路径,尚需进行n次试探。首先考虑路径(Vi, V1, Vj)是否存在(即判别弧(Vi, V1)和弧(V1, Vj)是否存在)。如果存在,则比较(Vi, Vj)和(Vi, V1, Vj)的路径长度,较短者为从Vi到Vj的中点顶点的序号不大于1的最短路径。假如在路径上再增加一个顶点V2,也就是说,若(Vi,…,V2)和(V2,...,Vj)分别是当前找到的中间顶点的序号不大于1的最短路径,那幺(Vi,...,V2,...,Vj)就有可能是从Vi到Vj的中间顶点的序号不大于2的最短路径。将它和已经得到的从Vi 到Vj的中间顶点的序号不大于1的最短路径相比较,从中选出中间顶点的序号不大于2的最短路径之后,再增加一个顶点V3,继续进行试探。依次类推,在经过n次比较之后,最后求得的必是从Vi 到Vj的最短路径。按此方法,可同时求得各对顶点间的最短路径。算法共需3层循环,总的时间複杂度是O(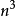 ) 。
) 。
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯