非常返状态
非常返状态(non-recurrent state)亦称瞬时状态,不是常返状态的状态。换句话说,马尔可夫链的状态i称为非常返的,如果链从状态i出发,它将以正的机率不再返回i,这又等价于说不管链从哪一个状态出发,以机率1它最多只能经过状态i有限多次。
基本介绍
- 中文名:非常返状态
- 外文名:non-recurrent state
- 学科:数学
- 适用场合:马尔地夫链
- 别称:瞬时状态
- 相关名词:常返状态
简介
设任意的 称
称 为马氏链在0时从状态i出发,经n步转移后,首次到达状态j的机率。简称首达机率。
为马氏链在0时从状态i出发,经n步转移后,首次到达状态j的机率。简称首达机率。


记 ,称为马氏链在0时从状态i出发,永远不能转移到
,称为马氏链在0时从状态i出发,永远不能转移到 状态j的机率。
状态j的机率。


又记 ,称
,称 为马氏链在0时从状态i出发,经有限步转移后终究到达状态j的机率(也称迟早机率)。
为马氏链在0时从状态i出发,经有限步转移后终究到达状态j的机率(也称迟早机率)。




设状态

(1)若 则称状态i是常返的(返回的);
则称状态i是常返的(返回的);

(2)若 则称状态i是非常返的(滑过状态)。
则称状态i是非常返的(滑过状态)。

当i为常返态时,也就有

即 构成机率分布,则相应的数学期望为
构成机率分布,则相应的数学期望为


则 表示马氏链从状态i出发首次再返回状态i的平均时间(或平均转移步数)。
表示马氏链从状态i出发首次再返回状态i的平均时间(或平均转移步数)。

利用量 可以进一步定义状态类型:
可以进一步定义状态类型:

(1)若 则称状态i为正常返状态;
则称状态i为正常返状态;

(2)若 则称状态i为零常返状态(消极常返状态)。
则称状态i为零常返状态(消极常返状态)。

状态类型的判断



定理
定理1
设状态 ,则
,则

(1)状态i是常返的( )充要条件为
)充要条件为


(2)状态i是非常返的( )充要条件为
)充要条件为


定理2
齐次马氏链的状态空间S可唯一地分解为有限或可列无限多个互不相交的状态子集的并。即

其中D是所有非常返状态构成的状态子集。

每个状态子集中的状态有着相同的状态类型:即 或者均为零常返,或者均为正常返非周期,或者均为正常返周期且周期相同。
定理3
设X是状态有限的齐次马氏链, 则
(1) X的非常返状态集D不可能是闭集;
(2) X不存在零常返状态;
(3) 若X是不可约的, 则X所有的状态都是正常返的。
举例
设状态空间S={1, 2, 3, 4}的马尔可夫链,它的一步转移机率矩阵为
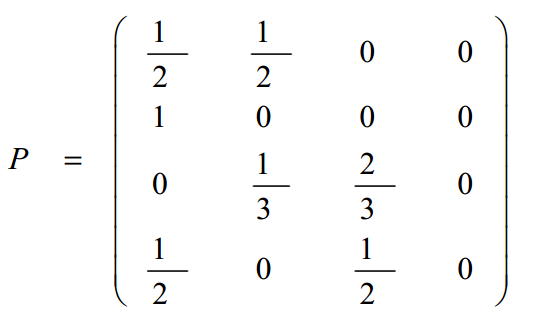
试分析马氏链的状态的常返与否。
解:马氏链的状态转移图为
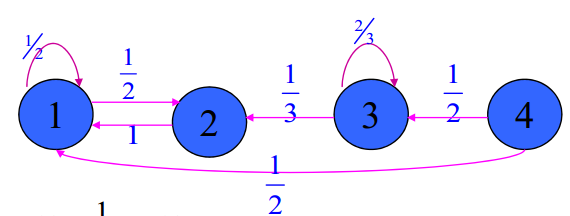
因为

所以 ,所以状态常返。
,所以状态常返。

又 ,故状态1正常返。
,故状态1正常返。

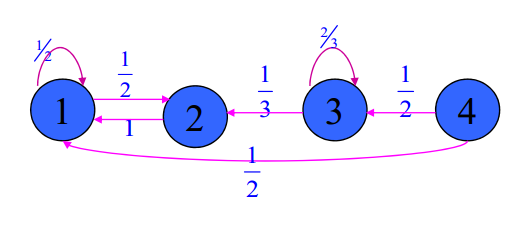
因为

所以 ,故状态3非常返。
,故状态3非常返。

类似可以讨论状态2和4。
因此可用下面的图来表示各状态的关係:
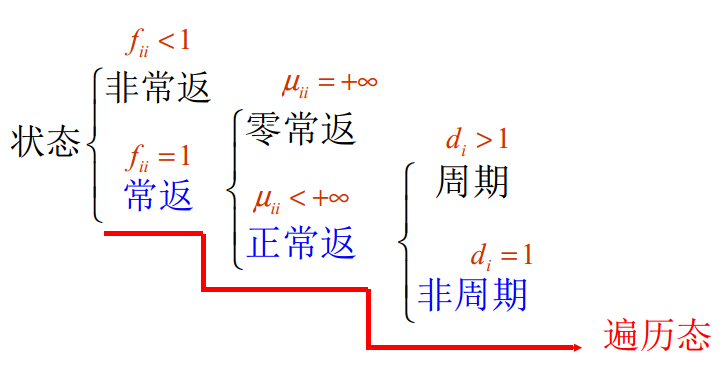
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯