网路路由
计算机网路有效地完成了网路资源、数据的共享,实现了软体和硬体相互协调的作用。网路路由将网路连线起来并将网路信息导向其他网路上,通常网路信息全自动寻找多个路由器,并选择效率最高的路由。网路路由器是计算机网路的重要组成部分,主要服务于网路间的连线,进行路由的选择等活动。网路路由通过对信息进行过滤、转发等,把两个或更多的网路连线起来,从而在计算机间连线起有效的网路,通过选择合适的路由路线,以最快的速度,将信息从一个网路层输送至另外一个网路层。
基本介绍
- 中文名:网路路由
- 外文名:network route
- 领域:计算机
- 释义:连线网路并将信息导向其他网路
- 据网路性质:分有线网路路由、无线网路路由等
- 据通信方式:分单播路由、多播路由等
网路路由的概念
给定网路G(V,E),V是节点集,V =N,E是边集,E =M。P是路径集对源节点S∈V及目的节点T∈V,找一条从S到T的路径p∈P,使得开销最小,而所有约束都能满足。设对每一个边(u,v)∈E,有损失函式cost(u,v)及权向量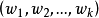 ,则要求最小化
,则要求最小化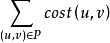 满足约束
满足约束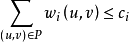 ,
,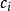 是常数,0≤i<k。
是常数,0≤i<k。
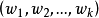
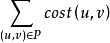
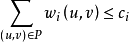
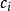
下一代高速广域网对实时流要求面向连结的路由。在运输层连结(呼叫)意味着终端用户之间的逻辑联繫及正确有序的数据投递。在网路层,连结意味着一条包含开关和链路的网路路径。同一连结的数据包沿路径按先进先出(FIFO)顺序传送。基于服务质量路由的约束包括链路约束、路径约束、树约束、时延约束等,而频宽则包括链路频宽及CPU频宽(节点把数据泵到链路上的最大速率)。
解这一问题的基础算法是Dijkstra算法和Bellman-Ford算法。Dijkstra算法是图论中寻找最短路径的算法,它实际上求出从源节点到系统中所有节点的最短路径。把它套用到网路路由,就嫌有点浪费,因为网路路由只要求从源节点到目的节点的最短路径。Bellman-Ford算法是寻找最短路径的分散式算法,允许边的权是负的,看来适合网路路由。但是,各节点的同步是一个问题。在不同步的情况下就可能得不到最优解。
网路路由的分类
网路路由有多种分类。
按网路性质
按网路性质可分为多计算机系统路由、有线网路路由和无线网路路由。计算机系统路由针对一种特定的拓扑结构,例如超立方体、格线,在某些节点或链路故障的情况下寻找最优通路。这些想法实质上与网际网路的路由非常类似。但是,今天,一个多计算机系统也许是一个超级大型机,用乙太网连线。再考虑到任意的拓扑结构,问题就更複杂了。
按通信方式
网路路由按通信方式分,可以分为单播路由(即端到端的路由)、多播路由(即端到目的节点集中的每一个节点的路由)及Anycast路由(即端到目的节点集中的任一个节点的路由)。
按路由算法
网路路由按路由算法来分,可以分为源路由算法、分散式路由算法和分级路由算法。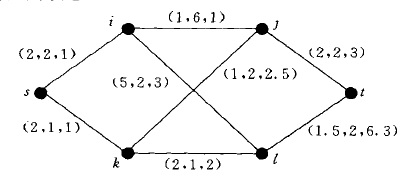 图1 网路状态
图1 网路状态
 图1 网路状态
图1 网路状态(1)源路由算法假定每个节点了解整个网路的全局状态。全局状态用链路状态协定通过广播获得,或用距离向量协定,用邻节点周期性交换距离向量获得。当要传送讯息时,源节点就决定了整条路径。
(2)分散式路由算法假定每个节点只了解它的邻节点的情况,即网路局部状态,包括排队延迟、传播延迟、剩余频宽等,根据路径的要求,只决定下一跳应走向哪里(见例1)。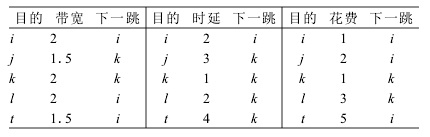 图2 节点S在距离向量下的全局状态
图2 节点S在距离向量下的全局状态
 图2 节点S在距离向量下的全局状态
图2 节点S在距离向量下的全局状态例1:考虑图1的网路,链路状态由(频宽、时延、花费)给定。图2给出了节点S在距离向量下的全局状态。
(3)分级路由算法假定网路节点分级,每个节点了解聚合的全局状态,即自己所在範围内的情况,而对远处的上级节点只了解大致情况。即每一物理节点保持聚合的网路影像(见例2)。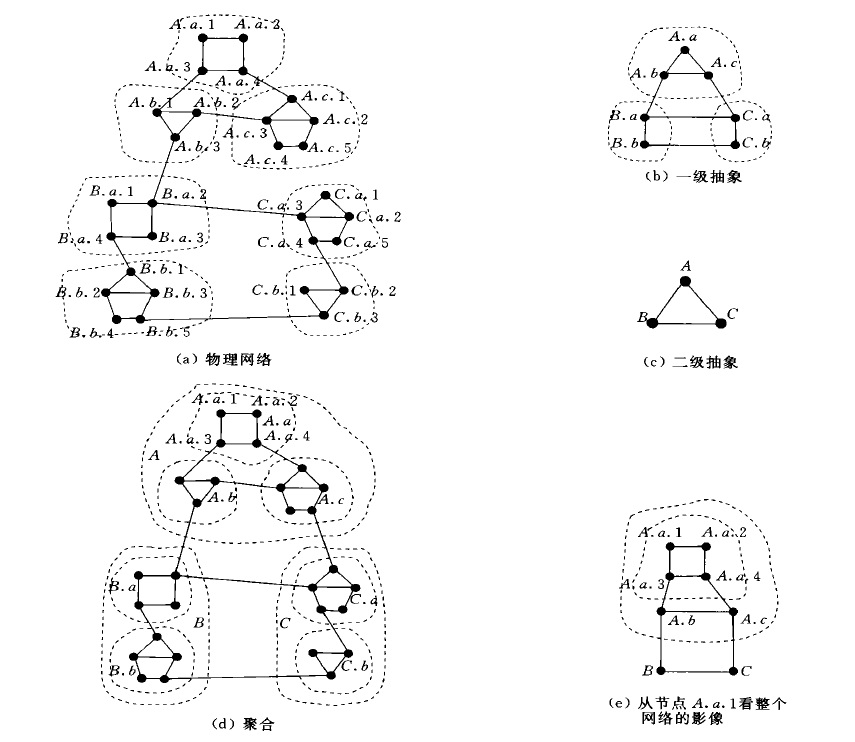 图3 分级网路
图3 分级网路
 图3 分级网路
图3 分级网路例2:图3给出一个分级网路模型。图(a)表示一个实际的网路,有29个节点;图(b)示出其第一级节点,共7个;图(c)示出第二级节点共3个,该物理网路经过聚合可以变成图(d);而从节点A、a、1来看整个网路则如图(e)所示。
按对路由的要求
网路路由按对路由的要求来分,可以分为尽力而为路由和基于服务质量路由。尽力而为路由是面向连线或带动态性能的无连线,以保证公平性、总吞吐量和平均回响时间为目标,在当前的网路环境下来选择最优路径。而基于服务质量的路由是对各流的包基于服务质量要求选择可用路径的过程,它面向连线,带资源预留,以满足各流的连线要求,减少呼叫阻塞。因此,它着重在满足约束,希望连线的数据传输不受其它连线的动态流量的影响。问题是网路永远是动态的,节点对全局网路服务质量状态的了解不精确、不实时,对路由的确定与预计就未见得完全正确。服务质量路由的代价主要包括两方面:一方面是计算开销。因为它需要更加複杂和频繁的路由计算。另一方面则是协定开销,因为它要分散式地提供和刷新与路由选择有关的网路资源状态信息。
路由选择计算
何时进行路由选择计算?一般来说是当每一次请求来到时触发路由选择。但是,如果在两次状态刷新之间,收到许多请求,也许事先计算好路由更加有效。当然也可以在收到状态刷新信息时计算路由。同时,路由选择必须有灵活性,以免由于路由而造成某些路径拥塞、某些路径又很空闲。状态刷新的触发也可以选择不同的时机。譬如现在的状态比原来变化超过50%就触发刷新,或者是,将可用频宽按大小分级,跳了一级就触发刷新。也可以周期性地定时触发。刷新内容包括刷新讯息的大小、通报的指标值的类型等都要在协定中规定。各种刷新方案各有优劣。刷新越及时,路由需要的网路状态信息就越精确,但刷新太频繁,增加网路负担。要在两个极端中折衷。在IPv6协定环境下,更多的地址和报头信息也会有助于网路路由。
单播路由算法
单播路由是指目的节点只有一个的路由。以剩余频宽和剩余快取空间为服务质量目标的路由选择是一类基于链路信息的路由,所选路径一般是根据路径上的瓶颈链路状态来决定的。例如图1中路径 的频宽是1,因为其瓶颈链路(i,j)的频宽是1。这一类路由可分为链路最优路由和链路约束路由。这两类基本路由问题可以用Dijkstra或Bellman-Ford多项式複杂性的算法解决。另一方面,以时延、时延抖动和花费为服务质量目标的路由选择是另一类所谓基于路径信息的路由。例如图1中
的频宽是1,因为其瓶颈链路(i,j)的频宽是1。这一类路由可分为链路最优路由和链路约束路由。这两类基本路由问题可以用Dijkstra或Bellman-Ford多项式複杂性的算法解决。另一方面,以时延、时延抖动和花费为服务质量目标的路由选择是另一类所谓基于路径信息的路由。例如图1中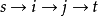 的路径时延是10,它是路径上各链路时延之和。从而引出另外两类基本路由问题:路径最优路由和路径约束路由。它们也可以用多项式複杂性的算法解决。
的路径时延是10,它是路径上各链路时延之和。从而引出另外两类基本路由问题:路径最优路由和路径约束路由。它们也可以用多项式複杂性的算法解决。

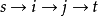
对于许多实际套用,路由不但对链路有要求,也对路径有要求,或者是对链路有多个要求,或者对路径有多个要求。例如最宽约束最小时延路由就是要求瓶颈链路最宽,而且路径时延最小。又如频宽约束和快取约束路由,如此等等,可以派生出许多组合的路由问题。其中只有两类有意义的NP难问题,即路径约束路径最优路由(PCPO)和多路径约束路由(MPC)。譬如时延约束最小花费路由,时延和时延抖动约束路由。若所有指标(除一个以外)全有界,或者全相关,则多项式时间可解。否则,这两类问题是NP难的。典型的单播路由算法有:
源路由算法
如果路由既有频宽约束,又有时延约束,源路由算法的複杂性就会增加。
分散式路由算法
分式式路由算法把源路由算法的计算开销分散到各个节点上,各个节点只需要了解局部的信息,作出局部的路径决策。这个算法一般用来找最短的最宽路径(瓶颈频宽最大的路径),但当不同节点的状态信息有矛盾时,该路由算法可能产生循环路由。
分级路由算法
当今网际网路的显着特徵是大型,而且天天在变化。分级路由恰恰是用来解决大型互连网源路由可扩展性问题的。对于ATM网路由的专用网路间接口标準(PNNI)就是分级的,每一个节点只保存一部分全局状态,许多节点集被聚合为逻辑节点。所以,这种聚合的全局状态的大小不过是整个全局状态大小的对数。因此,分级路由算法既能保持某些源路由算法的优点,又有许多分散式路由算法的优越性。因为路由计算由许多节点承担,分级路由算法先从源节点的聚合全局状态出发,从最高层开始逐步下走,直到第一层。确定了源节点所在最高层节点内的路由之后,交给下一个最高层节点的边界节点去确定在其内的路由,如此等等,直到目的节点。不难想像,路由算法的这种简化,必然带来路由质量的代价。聚合信息的不精确性严重影响路由的质量。考虑图3(e),很难估计从A、a、1到C中节点的时延,因为C的内部结构被隐藏了,并且,从A、c中的不同的节点到C中不同节点的时延可以是很不相同的,但在聚合的状态中只有一个时延值。所以,基于聚合信息的时延值是很不精确的。如果有多个服务质量约束,问题就更複杂。
按比例路由
选最短路径可以最小化资源利用,但这些被选路径由于常常被选上,而负载过重。选最轻负载路径可以平衡网路负载,但可能不是最短路径,因而浪费更多资源。另外,要求网路中节点保持精确的实时的服务质量状态是不现实的。事实上,保持精确的实时的服务质量状态只能靠及时更新,目前无法靠预测。更新时间太长,所得状态不精确;太短,开销又太大。选择最好路径还有同步的问题,一次刷新以后,空闲的链路会拥塞,而再一次刷新以后又会变得空闲。
基于策略的路由
边界网关协定(BGP)是网际网路域间路由协定。它允许自治系统独立地定义自己的路由策略,这就给网路路由提供了个性和灵活性。但是,同时也产生稳定性和收敛性的问题。有例子指出,基于策略的路由可能产生循环路由和路由振荡,这已经不光是一个路由的问题,还是一个协定的问题。
多播路由算法
多播路由的问题是:给定源节点S和目的节点集R、约束集C,也许还有一个最优目标,求最好的可行树,覆盖s和R的所有节点,满足约束C。例如在多播情况下,频宽最优的路由要求树的瓶颈链路频宽最大,时延约束路由则要求从传送者到所有目的节点的端到端延迟都小于一个给定值。
着名的斯坦(Steiner)树问题就是找花销最小的树,也就是最小花销多播路由问题。带约束的斯坦树问题也就是时延约束最小花销多播路由问题。这都是NP难的。时延和时延抖动双约束的多播路由问题也是NP难的。只有当所有指标(除一个以外)全有界,或者全相关,才会有多项式时间可解。
多播的源路由算法基于多播链路状态协定(MOSPF),该协定是单播链路状态协定(OSFP)的扩展。每一节点除了保存全局状态之外,还保存路由域内每一个多播组的成员信息。从而使最短路径多播路由可用Dijkstra算法解决,时延约束多播路由问题也较容易解决。
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯