MSE(均方误差)
不同科技领域有不同的含义:数理统计(两种),测量套用(一种),网路性能函式(一种)。
基本介绍
- 中文名:均方误差
- 外文名:Mean Square Error
- 所属学科:数学
- 拼音:jun fang wu cha
定义
定义1:方差分析中组内变异与误差自由度的商, .
.

定义2:参数估计中均方误差是指参数估计值与参数真值之差平方的期望值,记为MSE。
参数估计有无偏性準则、均方误差準则、有效性準则、相合性準则。
定义3:在相同测量条件下进行的测量称为等精度测量,例如在同样的条件下,用同一个游标卡尺测量铜棒的直径若干次,这就是等精度测量。对于等精度测量来说,还有一种更好的表示误差的方法,就是标準误差。设n个测量值的误差为ε1、ε2……εn,则这组测量值的标準误差σ等于:
标準误差定义为各测量值误差的平方和的平均值的平方根,与均方误差有联繫和区别。
定义4:MSE是网路的性能函式,网路的均方误差,叫"Mean Square Error"。比如有n对输入输出数据,每对为[Pi,Ti],i=1,2,...,n.网路通过训练后有网路输出,记为Yi。
均方误差合成
如果只有一组数据,样本方差就是均方误差
如果N个数据分为r组,且第 组的样本方差(样本方差参见百科)为
组的样本方差(样本方差参见百科)为 ,则全体的均方误差为
,则全体的均方误差为



其中,分子为误差平方和,N-r为自由度
事后检验
在事后两两检验时,需要用到Mse作为合成方差,这与两样本方差相同时的合成方差不同,因为Mse的合成方差可以包含不只两个组
均方误差
MSE的E代表误差error;类似的,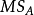 代表A因素的均方差。
代表A因素的均方差。
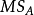
一般而言,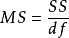
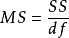
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯