
增乘开平方法
增乘开平方法是北宋数学家贾宪发明的开方法,原收《释锁算书》
基本介绍
- 中文名:增乘开平方法
- 发明者:贾宪
- 相关书籍:《释锁算书》等
- 被抄入卷:《永乐大典》
简介
增乘开平方法是北宋数学家贾宪发明的开方法,原收《释锁算书》一书。贾宪原作已佚,但他对数学的重要贡献,被南宋数学家杨辉引用,被抄入《永乐大典》卷一万六千三百四十四,幸得以保存下来。
术文
增乘开平方法,以商数乘下发递增求之。商第一位。上商得数以乘下发为乘方。命上商除实。上商得数以乘下发入乘方。一退为廉,下法再退。
商第二位。商得数以乘下发为隅。命上商除实讫。以上商乘下法入隅,皆名曰廉。一退,下法再退,以求第三位商数。
商第三位。用法如第二位求之
语译算法
初始
把待开方数赋值给变数实。
廉:0;
下法:以100为底,不大于实的最大幕数(主要是为了把实以每2个数分为一组设定)
商:0;
计算
步骤1:估商(x),求最大的整数x(商)使得:
(廉+x)*x <= 向下取整(实/下法), 0<=x<=9
(估出的x(商)即为开方后当前位的数值,)
步骤2:更新廉: 新廉=廉+x
步骤3:更新实: 新实=实-廉*x,若新实为0则表明开方完毕。
步骤4:再次更新廉:新廉=廉+x
步骤5:更新廉与下法:
新下法=下法/100(下法再退)
新廉=廉*10(与术文有差异,因为古法用算筹,现在用笔算,廉向下退一位,但相对于下法其实是进一位)
步骤6:以当前的 下法,廉,实 复上述步骤1~5,以求下一位的商,直到实=0或者达到要求的开方精度。
贾宪十进位制布位
- 算筹的布位。贾宪在纸上用书写方式将算筹码按十进位制布位。七万一千八百二十四分写两行
 贾宪十进位算筹布位
贾宪十进位算筹布位下行的步、十、百、千、万分离出来变为算筹的位值标籤;上行七一八二四成为十进位制数码。
然后将算筹码依次排在相应的位值标籤步、十、百、千、万之下:
 贾宪十进位制布位
贾宪十进位制布位杨辉算草
杨辉以七万一千八百二十四为例,列出详细算草。 算草分四行,被除数放在第二行,称为实,第一行是商,第四行为下法,第三行是廉。 将算筹放在第四行万字之下。 贾宪增乘开平方动画
贾宪增乘开平方动画
 贾宪增乘开平方动画
贾宪增乘开平方动画
初始 |  杨辉算草 杨辉算草 |
计算(第一轮) | |
经过步骤1,2,3后的算筹结果: 1估计第一个商数得2,将安置在第一行百位置之上。 2将上商2乘下法1,得数2,放在第三行廉。 3跟新实,实-廉*商数*下法(算筹中廉数是乘下法后的数,所以不用再乘下法) 7-2*2=3 |  杨辉算草 杨辉算草 |
经过步骤4,5后的算筹结果: 4跟新廉=2+2=4 5下法与廉下移 退下法两位,退廉1位 |  杨辉算草 杨辉算草 |
步骤6,进入第二轮计算商的下一位置,重複步骤1~5 | |
进过步骤1,2 1估商得6 2跟新廉:40+6=46 |  杨辉算草 杨辉算草 |
步骤3,跟新实 318-6*46=42 |  杨辉算草 杨辉算草 |
步骤4,更新廉 46+6=52 |  杨辉算草 杨辉算草 |
步骤5,6,并进入下一轮步骤1,2 5,更新下法与廉 退下法两位,退廉1位 6,1估商为8 2,跟新廉:520+8=528 |  杨辉算草 杨辉算草 |
步骤3,跟新实后实为0,开方完毕 | 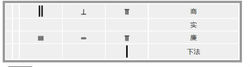 杨辉算草 杨辉算草 |
算草上的商即为开方后的结果:268 |
用增乘开平方法得到的解:

 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯