读书笔记摘抄新闻资讯Cis函式
cis函式又称纯虚数指数函式，是複变函数的一种，和三角函式类似。它的定义域是整个实数集，值域是单位複数，绝对值为1的複数。它是周期函式，其最小正周期为2π。其图像关于原点对称。
基本介绍
- 中文名：Cis函式
- 分类：数理科学
定义
上述文字称它以类似三角函式的形式来定义函式的原因是，就如同三角函式，他也算是一种比值，複数和其模的比值:
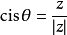
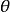
因此，当一複数的模为1，其反函式就是幅角（arg函式）。
cis函式可视为求单位複数的函式
cis函式的实数部分和余弦函式相同。
命名
由于cis函式的值为“余弦加上虚数单位倍的正弦”，取其英文缩写cosine andimaginary unitsine，故以cis来表示该函式。
欧拉公式
主条目：欧拉公式
在数学上，为了简化欧拉公式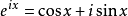
，因此将欧拉公式以类似三角函式的形式来定义函式，给出了cis函式的定义：
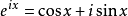
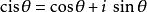
并且一般定义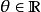域为
，值域为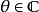
。
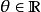
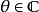
当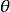
值为複数时，cis函式仍然是有效的，所以有些人可利用cis函式将欧拉公式推广到更複杂的版本。
指数定义
跟其他三角函式类似，可以用e的指数来表示，依照欧拉公式给出: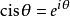
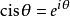
反函式
cis的反函式: arccis x，当代入模为1的複数时，所得的值是其辐角
类似其他三角函式，cis的反函式也可以用自然对数来表示
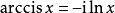
当一複数经过符号函式后代入arccis x可得辐角。
恆等式
cis函式的倍角公式似乎比三角函式简单许多。
双曲cis函式
一般会将双曲cis函式定义成:
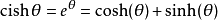
定义域和值域皆为实数，但若定义双曲複数，
考虑数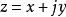
，其中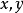
是实数，而量{\displaystyle j}不是实数，但{\displaystyle j^{2}}是实数。
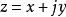
主条目：双曲複数
选取{\displaystyle j^{2}=-1}，得到一般複数。取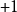
的话，便得到双曲複数。
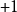
而双曲複数有对应的欧拉公式: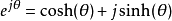
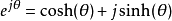
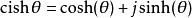
因此双曲cis函式得到的值为双曲複数，相反的若将其反函式带入模为一的双曲複数可得其辐角。
如此一来，值域将会变成四元数。
参见
- 正弦
- 余弦
- 複数 (数学)
- 三角函式
- 三角函式恆等式
- 欧拉公式