
直方图规定化
所谓直方图规定化,就是通过一个灰度映像函式,将原灰度直方图改造成所希望的直方图。所以,直方图修正的关键就是灰度映像函式。直方图规定化是用于产生处理后有特殊直方图的图像方法。
理想情况下,直方图均衡化实现了图像灰度的均衡分布,对提高图像对比度、提升图像 亮度具有明显的作用。在实际套用中,有时并不需要图像的直方图具有整体的均匀分布,而 希望直方图与规定要求的直方图一致,这就是直方图规定化。它可以人为地改变原始图像直方图的形状,使其成为某个特定的形状,即增强特定灰度级分布範围内的图像。
基本介绍
- 中文名:直方图规定化
- 外文名:Histogram specification
- 又称:直方图匹配
概述
图像直方图是图像处理中一种十分重要的分析工具,它描述了一幅图像的灰度级内容。从数学上来说,图像直方图是图像各灰度值统计特性与图像灰度值的函式,它统计一幅图像中各个灰度级出现的次数或机率;从图形上来说,它是一个二维图,横坐标表示图像中各个像素点的灰度级,纵坐标为各个灰度级上图像像素点出现的次数或机率,它是图像最基本的统计特徵。
直方图有以下性质:
(1) 直方图是一幅图像中各像素灰度出现频次的统计结果,它只反映图像中不同灰度值出现的次数,而不反映某一灰度所在的位置。
(2) 任何一幅图像,都有惟一确定的与它对应的直方图,但不同的图像可能有相同的直方图。
(3) 由于直方图是对具有相同灰度值的像素统计得到的,因此,一幅图像各子区的直方图之和就等于该图像全图的直方图。
我们知道,直方图均衡化处理有良好的图像增强效果。从实现算法上可以看出,其优点主要在于能自动增强整幅图像的对比度,但具体的增强效果也因此不易控制,只能得到全局均衡化处理的直方图。然而在实际套用中,往往要根据不同的要求得到特定形状的直方图分布,以有选择地对某灰度範围进行局部的对比度增强,即想要得到已知直方图的增强图像。此时,可以採用直方图的规定化处理,通过选择合适的规定化函式取得期望的效果。直方图规定化就是针对这种思想提出来的一种直方图修正增强方法。所以,从某种意义上,直方图规定化可看作是直方图均衡化方法的改进。
基本原理
直方图规定化的目的就是调整原始图像的直方图使之符合某一规定直方图的要求.设 Pr(r)和Pz(z)分别表示原始灰度图像和目标图像的灰度分布机率密度函式.根据直方图规 定化的特点与要求,应使原始图像的直方图具有Pz(z)所表示的形状。因此.建立Pr(r)和 Pz(z)之间的关係是直方图规定化必须解决的问题。
根据直方图均衡化理论,首先对原始图像进行直方图均衡化处理.即求变换函式
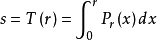
现假定直方图规定化的目标图像已经实现,因此,对于目标图像也採用同样的方法进行均衡化处理,因而有

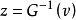

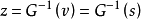
直方图规定化方法
根据上述理论推导,可以得出直方图规定化处理的一般步骤如下:
(1) 根据直方图均衡化原理,对原始图的直方图进行灰度均衡化处理;
(2) 规按照目标图像的机率密度函式Pz(z),求解目标图像进行均衡化处理的变换函式G(z);
(3) 用原始图像均衡化中得到的灰度级s代替v,求解逆变换z=G-1(s)。
经过上述处理得到的目标图像的灰度级将具有事先规定的机率密度Pz(z)。上述变换过程中所包含的两个变换函式T(r)和G-1(s)可形成複合函式,即可表示为
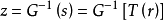
由此可知,无需进行直方图均衡化运算就可以直接实现直方图规定化处理,通过複合函式关係有效的简化了直方图规定化处理过程,求出T(r)和G-1(s)之间的複合函式关係就可以直接对原始图像进行变换。
效果示例
图3.3.2给出直方图规定化的一个示例,这里利用如图3.3.2(b)所示的规定化函式对原始图进行直方图规定化的变换,得到的 结果见图3.3.2(c)[其直方图见图3.3.2(d)所示]。由于规定化函式在高灰度区的值较大,所以与图 3.2.3相比,变换的结果图像比均衡化更亮,对应于均衡化图中较暗区域的一些细节更为淸晰。从直方图上看高灰度值一边更为密集。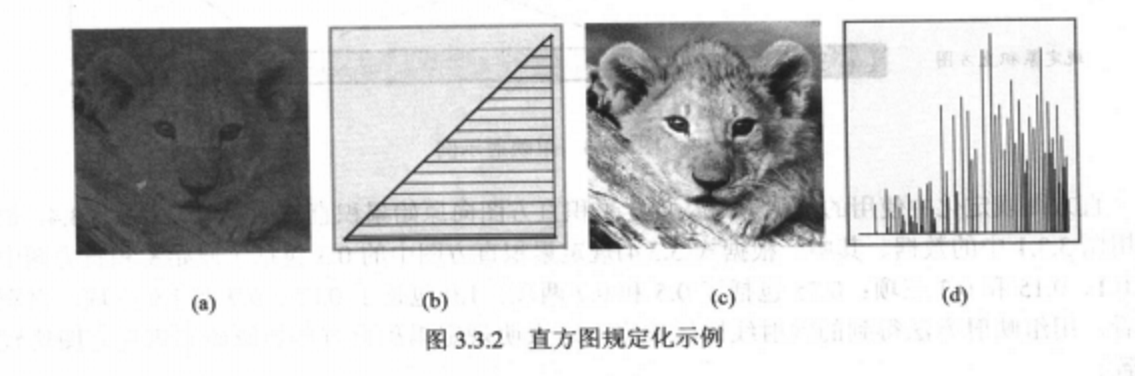

套用举例
直方图规定化,设计程式如下图:

程式运行结果如图4.4所示:

 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯