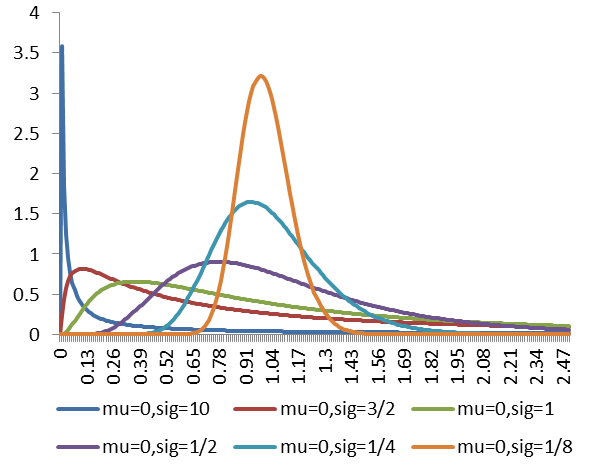
累积分布函式
累积分布函式(Cumulative Distribution Function),又叫分布函式,是机率密度函式的积分,能完整描述一个实随机变数X的机率分布。一般以大写CDF标记,,与机率密度函式probability density function(小写pdf)相对。
基本介绍
- 中文名:累积分布函式
- 外文名:cumulative distribution function
- 定义:F(a)=P(x<=a)
- 归类:数学函式
- 缩写:CDF
定义
对于所有实数 ,累积分布函式定义如下:
,累积分布函式定义如下:


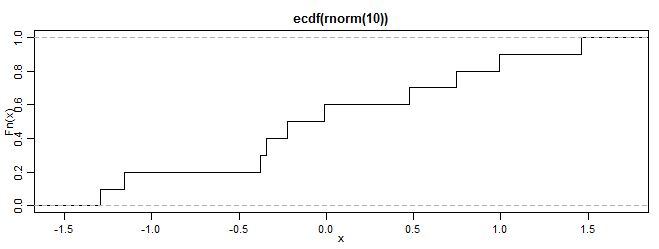 图1.累积分布函式
图1.累积分布函式性质
1.有界性
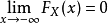
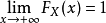
2.单调性
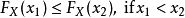
3.右连续性
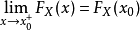
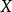
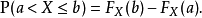

反函式
若累积分布函式F是连续的严格增函式,则存在其反函式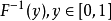 。累积分布函式的反函式可以用来生成服从该随机分布的随机变数。
。累积分布函式的反函式可以用来生成服从该随机分布的随机变数。
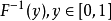
设若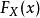 是机率分布X的累积分布函式,并存在反函式
是机率分布X的累积分布函式,并存在反函式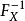 。若a是[0,1)区间上均匀分布的随机变数,则
。若a是[0,1)区间上均匀分布的随机变数,则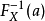 服从X分布。
服从X分布。
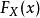
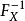
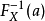
互补累积分布函式
互补累积分布函式(complementary cumulative distribution function、CCDF),是对连续函式,所有大于a的值,其出现机率的和。
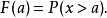
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯