
皮亚诺曲线
皮亚诺曲线(Peano curve)是一曲线序列的极限。只要恰当选择函式,画出一条连续的参数曲线,当参数t在0、1区间取值时,皮亚诺曲线将遍历单位正方形中所有的点,得到一条充满空间的曲线。 皮亚诺曲线是一条连续而不可导的曲线。
基本介绍
- 中文名:皮亚诺曲线
- 外文名:Peano curve
- 提出者:朱塞佩•皮亚诺
- 原像维度:1维
- 像的维度:2维
- 性质:曲线的像充满正方形
皮亚诺曲线的发现
皮亚诺(Peano)曲线是一条能够填满正方形的曲线。
1890年,义大利数学家皮亚诺(GiuseppePeano)发现能填满一个正方形的曲线,叫做皮亚诺曲线。皮亚诺对区间上的点和正方形上的点的对应作了详细的数学描述。实际上,正方形的这些点对于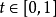 ,可规定两个连续函式
,可规定两个连续函式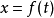 和
和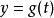 ,使得x和y取属于单位正方形的每一个值。后来,希尔伯特作出了这条曲线。
,使得x和y取属于单位正方形的每一个值。后来,希尔伯特作出了这条曲线。 皮亚诺曲线
皮亚诺曲线
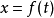
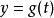
 皮亚诺曲线
皮亚诺曲线维数的认识
在传统概念中,曲线的维数是1维, 正方形是2维。按照通常的理解,没有宽度的一维的曲线是不可能填满2维的方格的。
皮亚诺曲线说明我们对维数的认识是有缺陷的,有必要重新考察维数的定义。这就是分形几何考虑的问题。在分形几何中, 维数可以是分数的叫做分数维度。
此外皮亚诺曲线是连续的但处处不可导的曲线。因此如果我们想要研究传统意义上的曲线, 就必须加上可导的条件,以便排除像皮亚诺曲线这样的特例。
集合论观点
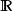
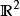
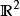
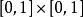
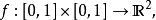
同理存在一个一一映射
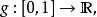
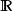
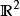
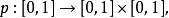
但该映射不一定是连续的。Peano曲线给出了一个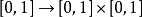 的连续满射,一般来说,一维的曲线是不可能填满2维的方格的。但是皮亚诺曲线恰恰给出了可行的例子。
的连续满射,一般来说,一维的曲线是不可能填满2维的方格的。但是皮亚诺曲线恰恰给出了可行的例子。
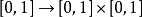
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯