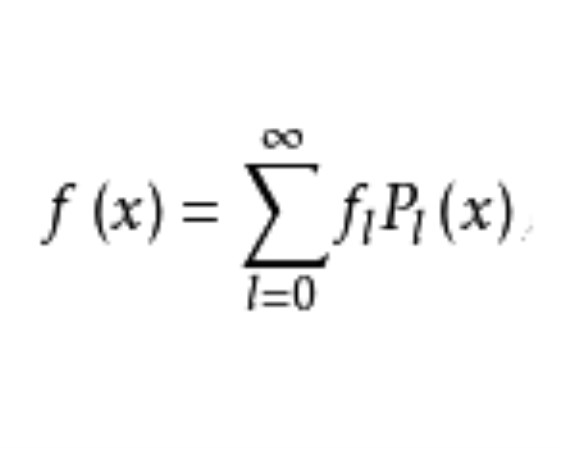
广义傅立叶级数
广义傅立叶级数(generalized Fourier series)是特殊的正交级数,函式f(r)在区间[0,a]上具有二阶连续导数,则f(r)可以展开成以贝塞尔函式为基的广义傅立叶级数。
基本介绍
- 中文名:广义傅立叶级数
- 外文名:generalized Fourier series
- 所属学科:数学
- 简介:一种特殊的正交级数
- 相关概念:贝塞尔(Bessel)函式
基本介绍
对于定义在区间[-1,1]上的具有二阶连续导数的函式f(x),当它与P,(z)具有相同的边界条件时,可按Pl(x)展为绝对且一致收敛的级数,
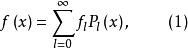
在式(1)两端乘以Pk(x)并在区间[-1,1]上积分,利用正交归一性,得

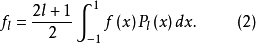
如果将变数x换回θ,则式(1)和式(2)变为
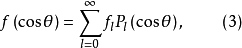
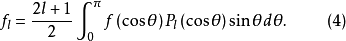
例题解析
【例1】以勒让德多项式为基,在[-1,1]上将函式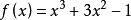 展为广义傅立叶级数。
展为广义傅立叶级数。
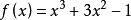
解:这里我们当然可以按照式(1)和式(2)将f(x)展开,但是由于f(x)是比较简单的三次多项式形式,应该可以表示为P0(x),P1(x),P2(x)和P3(x)的线性组合,从而可以利用待定係数法确定广义傅立叶係数,不妨设
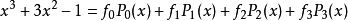


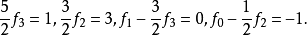

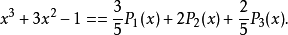
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯