多重傅立叶级数
傅立叶级数是一类特殊的三角级数。当n≥2时,常称σ(f)为多重傅立叶级数。
基本介绍
- 中文名:多重傅立叶级数
- 外文名:multiple Fourier series
- 适用範围:数理科学
简介
傅立叶级数
傅立叶级数是一类特殊的三角级数。
设f是在Tn={x=(x1,x2,...,xn)|-π≤xj<π,j=1,2,...,n}上勒贝格可积,对每个变元都以2π为周期的实值函式(函式取实值的限制不是本质的),定义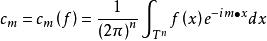 为f的傅立叶係数,这里m=(m1,m2,...,mn)是n元整点,其全体记为Zn,m·x=m1x1+m2x2+...+mnxn。三角级数
为f的傅立叶係数,这里m=(m1,m2,...,mn)是n元整点,其全体记为Zn,m·x=m1x1+m2x2+...+mnxn。三角级数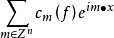 称为f的傅立叶级数,用σ(f)表示。
称为f的傅立叶级数,用σ(f)表示。
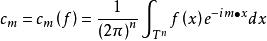
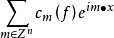
定义
当n≥2时,常称σ(f)为多重傅立叶级数。
推广
在单变元情形,常把σ(f)写成下述实形式: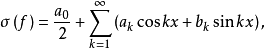 其中
其中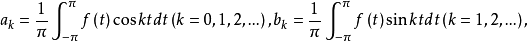 ak和bk分别称为f的余弦和正弦傅立叶係数。
ak和bk分别称为f的余弦和正弦傅立叶係数。
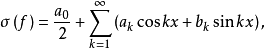
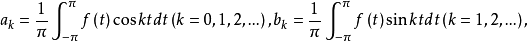
三角级数
在数学中,傅立叶级数是一种三角级数,傅立叶级数也常称为三角级数。但并不是所有三角级数都是傅立叶级数。
一个有趣的问题是给定一个三角级数,当x取什幺值时级数收敛。格奥尔格·康托尔在1870年证明了这一定理。如果三角级数的和函式是零,那幺,该三角级数的各项係数均为零。因此,如果两个三角级数的和函式相等,那幺它们的各项係数也相等。
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯