
DFS(离散傅立叶级数)
DFS也即离散傅立叶级数,又称离散时间傅立叶级数即DTFS,T代表时间。
基本介绍
- 中文名:离散傅立叶级数
- 外文名:discrete-time Fourier series
- 类型:公式
- 特点:周期性,离散性
简介
连续周期信号的连续傅立叶级数有着无穷多的离散频率分量,相邻分量的间距由信号的周期决定,等于1/T(角度,弧度乘2π)。
和连续周期信号相比,离散周期信号的离散傅立叶级数的频谱是周期性的,因为时域的连续对应于频率的非周期,时域的离散对应于频率的周期。所以我们只需要在(0,2π)的频域区间上取N个点就可以完整表示出来了。这是连续周期信号和离散周期信号傅立叶级数的最根本区别。
级数公式
DFT即是Discrete Fouriers Transform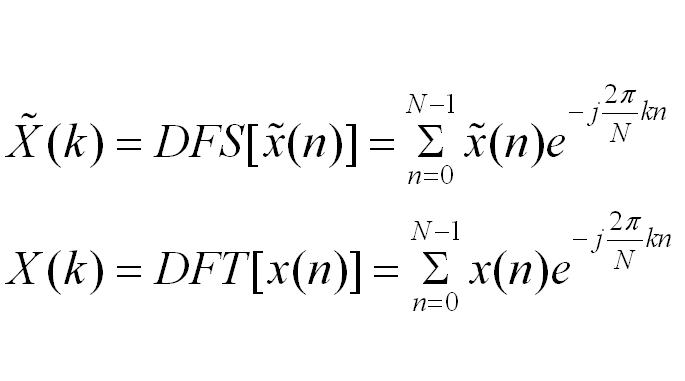
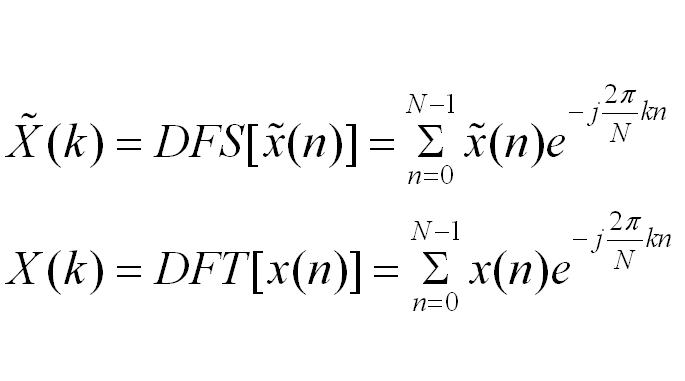
周期为N的周期序列x[k],其离散傅立叶级数为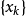 :
:
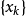
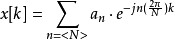
其中,DFS的逆变换序列:
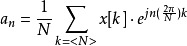
进一分析
连续周期信号的离散化(下面的讨论中, ):
):

首先,在傅立叶级数一文中,我们知道函式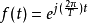 是对于任意的T是周期为T的函式,然而其对应的离散信号则不一定是周期的,可以证明,只有当
是对于任意的T是周期为T的函式,然而其对应的离散信号则不一定是周期的,可以证明,只有当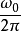 是有理数时,离散信号f[n]才是周期函式。
是有理数时,离散信号f[n]才是周期函式。
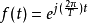
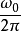
其次,在满足条件1的前提下,连续周期信号<math>f_k(t)</math>对应的离散信号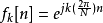 对k也具有周期性,其周期为N,即
对k也具有周期性,其周期为N,即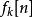 中只有N个不同的序列。
中只有N个不同的序列。
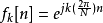
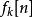
从离散时间傅立叶变换的係数公式我们可以看出,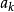 也是对k周期为N的函式。
也是对k周期为N的函式。
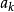
离散傅立叶变换实际上是离散时间傅立叶级数在主值区间上的取值。我们注意到,离散傅立叶变换是对非周期函式f[n]进行的,如果我们对f[n]的定义拓广为周期函式f'[n]: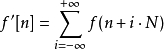 。并且当
。并且当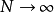 时,f'[n]实际上就是f[n],那幺我们现在可以求出f'[n]的傅立叶级数。同样,当
时,f'[n]实际上就是f[n],那幺我们现在可以求出f'[n]的傅立叶级数。同样,当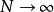 时无穷级数变成了积分,得到的结果是一个连续的周期函式
时无穷级数变成了积分,得到的结果是一个连续的周期函式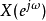 (正如离散傅立叶变换一文中所述),这就是f[n]的离散时间傅立叶变换。这时,只需在它的主值区间上採样,就可以得到离散傅立叶变换的变换序列。
(正如离散傅立叶变换一文中所述),这就是f[n]的离散时间傅立叶变换。这时,只需在它的主值区间上採样,就可以得到离散傅立叶变换的变换序列。
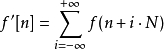
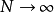
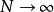
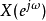
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯