内部(数学名词)
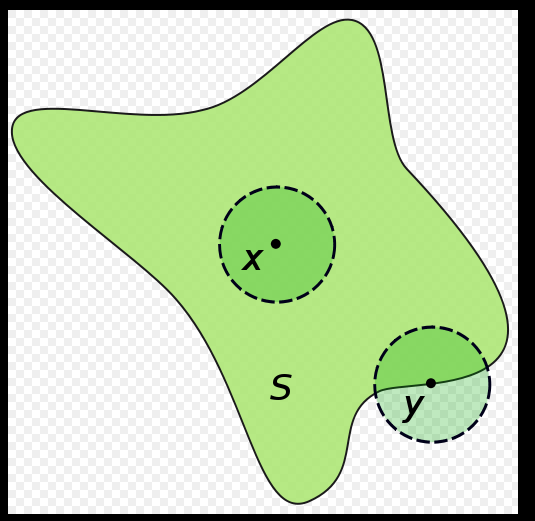
数学上,集合 S 的内部(又称开核)含有所有直观上“不在 S 的边界上”的 S 的点。S 的内部中的点称为 S 的内点。
基本介绍
- 中文名:内部
- 外文名:interior
- 又名:开核
- 套用学科:数学
- 相关术语:内点
- 套用领域:拓扑空间
定义
数学上,集合 S 的内部(又称开核)含有所有直观上“不在 S 的边界上”的 S 的点。S 的内部中的点称为 S 的内点。
若 S 为欧几里德空间的子集,则 x 是 S 的内点,若存在以 x 为中心的开球被包含于 S。
这个定义可以推广到度量空间X 的任意子集 S。具体地说,对具有度量 d 的度量空间 X,x 是 S 的内点,若对任意 r > 0,存在 y 属于 S,且 d(x, y) < r。
这个定义也可以推广到拓扑空间,只需要用邻域替代“开球”。 设 S 是拓扑空间 X 的子集,则 x 是 S 的内点,若存在 x 邻域被包含于 S。注意,这个定义并不要求邻域是开的。
等价地,S的内部是S补集的闭包的补集。内部的概念在很多情况下和闭包的概念对偶。
一个集合的外部是它补集的内部,等同于它闭包的补集;它包含既不在集合内,也不在边界上的点。一个子集的内部、边界和外部一同将整个空间分为三块(或者更少,因为这三者有可能是空集)。内部和外部总是开的,而边界总是闭的。没有内部的集合叫做边缘集。
拓扑学
设集合X及其幂集P(X),映射i: P(X)→P(X)称为内部运算元,若且唯若其满足以下内部公理:
- i1:∀A⊆X,i(A)⊆A;
- i2:∀A⊆X,i(A)=i(i(A));
- i3:∀A,B⊆X,i(A∩B)=i(A)∩i(B)
- i4:i(X)=X;
其中对于X的子集A,i(A)称为A的内部,i(A)中的点称为A的内点。
从内部运算元出发可以定义拓扑,这和从开集,闭集,闭包,邻域,导集,基等概念出发定义拓扑的方式是等价的。
- 开集
X的子集A称为开集,若且唯若i(A)=A; - 闭集
X的子集A称为闭集,若且唯若i(X-A)=X-A; - 闭包运算元,闭包,触点
- 闭包运算元c:P(X)→P(X)定义为∀A⊆X,c(A)=X-i(X-A)。其中c(A)称为A的闭包,c(A)中的点称为A的触点。闭包运算元是内部运算元的对偶概念,闭包是内部的对偶概念,触点是内点的对偶概念。
- 邻域
X的子集A,B,称A是B的邻域,若且唯若B⊆i(A)。 - 边界,边界点
边界运算元∂
P(X)→P(X)定义为∀A⊆X,∂A=A-i(A)。其中∂A称为A的边界,∂A中的点称为A的边界点。
内点
- 令S为欧几里得空间的子集。若存在以x为中心的开球被包含于S,则x是S的内点。
- 这个定义可以推广到度量空间X的任意子集S。具体地说,对具有度量d的度量空间X,x是S的内点,若对任意不属于S或在S边界上的y,都有d(x,y) >0。
- 这个定义也可以推广到拓扑空间,只需要用邻域替代“开球”。 设S是拓扑空间X的子集,则x是S的内点,若存在x邻域被包含于S。注意,这个定义并不要求邻域是开的。
集合的内部
集合 S 的内部是 S 的所有内点组成的集合。S 的内部写作 int(S)、Int(S) 或 S int(S) 是 S 的开子集。
int(S) 是所有包含于 S 的开集的并集。
int(S) 是包含于 S 的最大的开集。
集合 S 是开集,若且唯若S = int(S)。
int(int(S)) = int(S)。(幂等)
若 S 为 T 的子集,则 int(S) 是 int(T) 的子集。
若 A 为开集,则 A 是 S 的子集,若且唯若 A 是 int(S) 的子集。
有时候,上述第二或第三条性质会被作为拓扑内部的定义。
结论和性质
- ∀A,B⊆X,A⊆B ⇒ i(A)⊆i(B)。
- ∀A,B⊆X,i(A∪B)⊇i(A)∪i(B)。
- ∀A,B⊆X,A是开集 ⇒ ( A⊆B ⇔ A⊆i(B) )。(i(B)是包含于B的最大开集。)
- ∀B⊆X,i(B) = ∪{A:A是开集,A⊆B};(i(B)是B中所有开集之并。)
举例
在任意空间,空集的内部是空集。
对任意空间 X, int(X) = X.
若 X 为实数的欧几里德空间 R,则 int([0, 1]) = (0, 1)。
若 X 为实数的欧几里德空间 R,则有理数集合 Q 的内部是空集。
若 X 为複平面C = R 在任意欧几里德空间,任意有限集合的内部是空集。
在实数集上,除了标準拓扑,还可以使用其他的拓扑结构。
若 X = R,且 R 有下限拓扑,则 int([0, 1]) = [0, 1)。
若考虑 R 中所有集合都是开集的拓扑,则 int([0, 1]) = [0, 1]。
若考虑 R 中只有空集和 R 自身是开集的拓扑,则 int([0, 1]) 是空集。
上述示例中集合的内部取决于背景空间的拓扑。接下来给出的两个示例比较特殊。
在任意离散空间中,由于所有集合都是开集,所以所有集合都等于其内部。
在任意不可分空间X 中,由于只有空集和 X 自身是开集,所以 int(X) = X 且对 X 的所有真子集A,int(A) 是空集。
内部运算元
内部运算元是闭包运算元的对偶,在如下意义上
- So=X\ (X\S)-,
还有
- S-=X\ (X\S)o
这里的X是包含S的拓扑空间,反斜槓指示补集。
因此,通过把集合替代为它的补集,闭包运算元和库拉托夫斯基闭包公理的抽象理论可以轻易的转换到使用内部运算元的语言中。
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯