雷诺传输定理
雷诺传输定理(Reynolds transport theorem),又称为传输方程式(Transport equation),用于描述流体(fluid)性质的变化。
基本介绍
- 中文名:雷诺传输定理
- 外文名:Reynolds transport theorem
- 又名:传输方程式
- 意义:描述流体(fluid)性质的变化
简介
雷诺传输定理也称为莱布尼兹-雷诺传输定理或雷诺定理,是以积分符号内取微分闻名的莱布尼兹积分律的三维推广。
雷诺传输定理得名自奥斯鲍恩·雷诺,用来调整积分量的微分,用来推导连续介质力学的基础方程。
考虑在时变的区域 积分
积分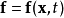 ,其边界为
,其边界为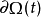 ,考虑上式对时间的积分:
,考虑上式对时间的积分:

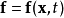
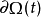
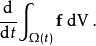
若要求上述积分的导数,会有两个问题,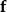 的时间相依性,及因
的时间相依性,及因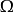 动态的边界而增加或减少的空间,雷诺传输定理提供了必要的框架。
动态的边界而增加或减少的空间,雷诺传输定理提供了必要的框架。
特点
传输方程式可用来定量地描述流场中流体性质的变化情形,譬如在一个控制容积(Control volume)之中含有某种流体。在经过一段时间 之后,若控制容积中流体的总体性质B有所改变,则其变化必定是下列两种原因所造成的: (1)总体性质B可能会因为本身的特性或外在因素的影响而产生随时间的变化,譬如流体中含有某种化学物质,该物质会因化学反应造成其质量B的变化,dB/dt即为该物质质量的变化率。又譬如B为流体的动量,在受到外力的状况下,流体的动量会有所改变。 (2)因为流体流动所造成的变化:当流体流经控制容积时,会带入或带出一部份的物质。当流出控制容积的总体性质大于流入量,则净流出量为正,会造成控制容积之中该总体性质的减少;反之,流入量大于流出量便会造成该总体性质的增加。
通用型式
要推导的雷诺传输定理是:
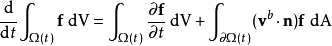
其中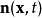 为向外的单位法向量,
为向外的单位法向量,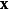 为区域中的一点,也是积分变数,
为区域中的一点,也是积分变数,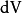 及
及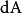 是
是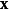 内的体积元素及表面元素,
内的体积元素及表面元素,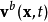 为面积元素的速度,不一定要是流速。函式
为面积元素的速度,不一定要是流速。函式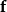 可以是张量、向量或标量函式。注意等式左边的积分只是时间的函式,因此可以用全微分。
可以是张量、向量或标量函式。注意等式左边的积分只是时间的函式,因此可以用全微分。
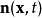
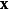
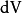
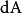
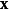
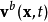
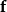
针对流体块的形式
在连续介质力学中,此定理常用在没有物质进来或离开的流体块或固体中。若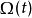 为一流体块,则存在速度函式
为一流体块,则存在速度函式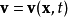 及边界元素符合下式:
及边界元素符合下式:
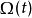
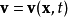
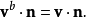
上式在替代后,可以得到以下的定理:
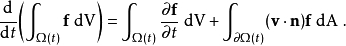
错误的引用
此定理常被错误的引用为只针对物质体积(material volume)的形式,若将只针对物质体积套用于物质体积以外的区域中,就会出现问题。
特别形式
简化
若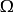 不随时间改变,则
不随时间改变,则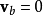 ,且恆等式化简为以下的形式:
,且恆等式化简为以下的形式:
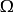
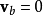
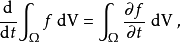
不过若用了不正确的雷诺传输定理,无法进行上述的简化。
在一维下的诠释及简化
此定理是积分符号内取微分的高维延伸,有些情形下可以简化为积分符号内取微分。假设f和y}和z无关,且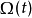 为
为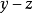 平面的单位方块,且有
平面的单位方块,且有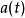 及
及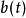 的极限,雷诺传输定理会简化为:
的极限,雷诺传输定理会简化为:
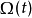
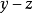
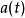
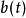
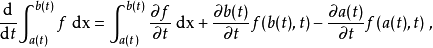
上述是由积分符号内取微分来的表示式,但x及t变数已经对调。
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯