直线(数学概念)
直线由无数个点构成。直线是面的组成成分,并继而组成体。没有端点,向两端无限延长,长度无法度量。直线是轴对称图形。
它有无数条对称轴,其中一条是它本身,还有所有与它垂直的直线(有无数条)对称轴。在平面上过不重合的两点有且只有一条直线,即不重合两点确定一条直线。在球面上,过两点可以做无数条类似直线。
构成几何图形的最基本元素。在D·希尔伯特建立的欧几里德几何的公理体系中,点、直线、平面属于基本概念,由他们之间的关联关係和五组公理来界定。
基本介绍
- 中文名:直线
- 外文名:straight line
- 所属学科:数学
- 所属领域:几何学
- 相关术语:直线方程
- 定义:由无数个点构成
直线方程
平面方程
一般式
适用于所有直线的方程:
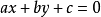

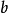
点斜式
知道直线上一点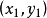 ,并且直线的斜率
,并且直线的斜率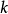 存在,则直线可表示为:
存在,则直线可表示为:
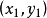
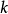

当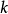 不存在时,直线可表示为:
不存在时,直线可表示为:
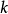
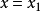
斜截式
知道直线在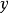 轴上截距为
轴上截距为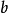 (即经过点
(即经过点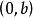 ),斜率为
),斜率为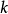 ,直线可表示为:
,直线可表示为:
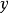
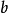
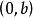
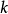
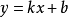
当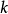 不存在时,直线可表示为:
不存在时,直线可表示为:
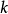
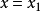
截距式
知道直线与 轴交于
轴交于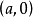 ,与
,与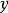 轴交于
轴交于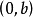 ,则直线可表示为:
,则直线可表示为:

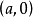
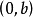
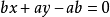
当 、
、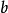 均不为0时,斜截式可写为
均不为0时,斜截式可写为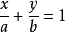

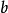
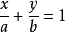
该表达式不适用于和任意坐标轴垂直的直线
两点式
知道直线经过点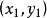 和点
和点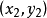 ,且斜率存在,则直线可表示为:
,且斜率存在,则直线可表示为:
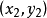
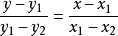
法线式
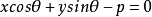
其中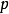 为原点到直线的距离,
为原点到直线的距离,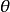 为法线与
为法线与 轴正方向的夹角
轴正方向的夹角
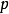
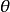

点方向式
知道直线上一点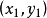 ,
,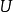 、
、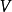 不等于0,并且直线不与
不等于0,并且直线不与 轴、
轴、 轴平行,则直线可表示为:
轴平行,则直线可表示为:
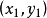
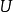
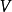


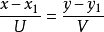
点法向式
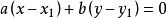
空间方程
1. 一般方程:
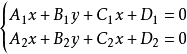
2. 点向式方程:
设直线方向向量为(m,n,p ),经过点( x0,y0,z0)
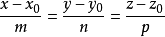
3. x0y式
x=kz+b,y=lz+b
有关内容
“角”
设平面e的法向量为c 直线m、n的方向向量为a、b
把平面ax+by+cz+d=0的法向量为(a,b,c);直线x=kz+b,y=lz+a的方向向量为(k,l,1)代入即可
则直线所成的角:m,n所成的角为a。
cosa=cos<a,b>=|a*b|/|a||b|
直线和平面所成的角: 设b为m和e所成的角,则b=π/2±<a,c>。sinb=|cos<a,c>|=|a*c|/|a||c|
平面两直线所成的角:设K(l1)=k1,K(l2)=k2(k1k2≠-1),tan<l1,l2>=(k1-k2)/(1+k1k2)
距离
异面直线的距离:l1、l2为异面直线,l1,l2公垂直线的方向向量为n、C、D为l1、l2上任意一点,l1到l2的距离为|AB|=|CD*n|/|n|
点到平面的距离:设PA为平面的一条斜线,O是P点在a内的射影,PA和a所成的角为b,n为a的法向量。
易得:|PO|=|PA|sinb=|PA|*|cos<PA,n>|=|PA|*(|PA*n|/|PA||n|)=|PA*n|/|PA|
直线到平面的距离为在直线上一点到平面的距离;
点到直线的距离:A∈l,O是P点在l上的射影,PA和l所成的角为b,s为l的方向向量。
易得:|PO|=|PA|*|sinb|=|PA|*|sin<PA,s>|=|(PA|2|s|2|-|PA*s|2)1/2/|s|
平面内:直线ax+by+c=0到M(m,n)的距离为|am+bn+c|/(a2+b2)1/2
平行直线:l1:ax+by+c=0,l2:ax+by+d=0,l1到l2的距离为|c-d|/(a2+b2)1/2
备注:
直线是曲线的暂短停留。
套用
点与直线
一般情况下,点与直线的距离,是指点到直线的最短距离,即垂直距离。
在二维直角坐标中,直线 Ax+By+C=0 与点 (p,q) 的最短距离为
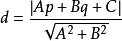
给出向量式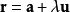 和 点
和 点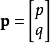 ,则有距离
,则有距离
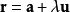
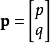
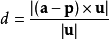
直线相交点
不考虑重合的情形,在二维平面中,两条相交直线可以相交或平行。
给定两条直线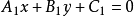 和
和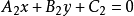 ,二者相交的条件是
,二者相交的条件是
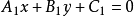
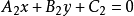
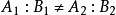
或等价地,
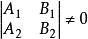
当中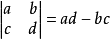 。
。
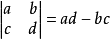
这时两线的相交点可从克莱姆法则求得
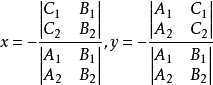
相交直线夹角
若两线相交,则会形成夹角。两线之间的夹角,通常指不大于90°的一只。
在二维平面上,给定直线y=mx+b,该线与x-轴的夹角为
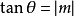
给定两条直线 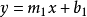 和
和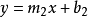 ,二者互相垂直若且唯若
,二者互相垂直若且唯若
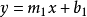
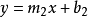
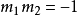
而其他情况,两线相交所形成的夹角 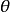 (
(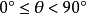 ),则由
),则由
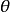
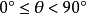
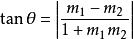
给定相交直线向量式 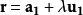 和
和 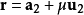 ,则有
,则有
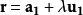
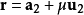
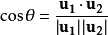
直线的距离
一般情况下,两条直线的距离,是指最短距离。
二维情况下,两条相交直线的距离必然为 0 。
若有两条平行直线 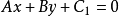 及
及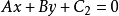 ,则有距离
,则有距离
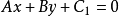
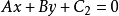
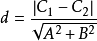
给定平行向量式 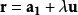 和
和 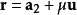 ,则有
,则有
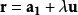
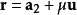
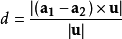
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯