切平面
在一定条件下,过曲面Σ上的某一点M的曲线有无数多条,每一条曲线在点M处有一条切线,在一定的条件下这些切线位于同一平面,称这个平面为曲面Σ在点M处的切平面(tangent plane)。点M叫做切点。
基本介绍
- 中文名:切平面
- 外文名:tangent plane
- 拼音:qiē píng miàn
- 领域:几何
性质
曲面Σ上过点M的所有曲线在点M处的切线都位于曲面Σ在切点M处的切平面。
证明
设正则参数曲S的方程为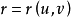 ,
,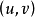 是曲面S上点的曲纹坐标,因此曲面S上的任意曲线L可以用参数方程
是曲面S上点的曲纹坐标,因此曲面S上的任意曲线L可以用参数方程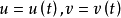 给出,将其视为
给出,将其视为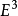 中的曲线,则其方程为
中的曲线,则其方程为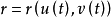 。
。 球面的切平面
球面的切平面
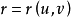
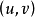
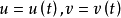
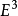
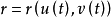
 球面的切平面
球面的切平面显然,根据定义,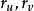 都是曲面S的切向量,假定P是曲线上对应t=0的点,因此曲面S在点P的切向量是
都是曲面S的切向量,假定P是曲线上对应t=0的点,因此曲面S在点P的切向量是
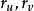
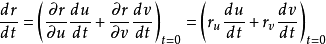
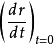
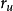
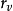
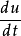
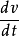
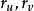
实际上,对于任意实数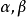 ,只要命曲线L为
,只要命曲线L为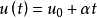 ,
,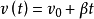 ,其中,
,其中,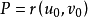 ,则曲线L在点P的切向量是
,则曲线L在点P的切向量是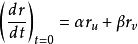 .
. 切平面
切平面
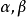
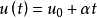
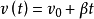
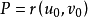
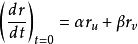
 切平面
切平面由于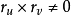 ,故
,故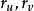 是线性无关向量,因此曲面在点P的切向量构成一个二维向量空间,这个空间称为曲面S在点P的切空间,记做
是线性无关向量,因此曲面在点P的切向量构成一个二维向量空间,这个空间称为曲面S在点P的切空间,记做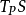 ,显然,
,显然,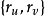 构成了空间
构成了空间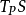 的一个基底。在空间
的一个基底。在空间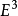 中经过点P、并且由空间S在点P张成的平面就是曲面S在点P的切平面,显然,曲面在点P的切平面是与曲面的参数表示无关的概念。
中经过点P、并且由空间S在点P张成的平面就是曲面S在点P的切平面,显然,曲面在点P的切平面是与曲面的参数表示无关的概念。
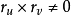
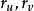
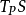
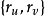
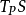
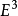
曲面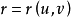 在点
在点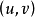 的切平面的参数方程是
的切平面的参数方程是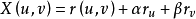 .
.
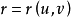
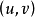
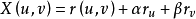
举例
平面的切平面为此平面自身。
锥面的所有切平面都经过一个定点
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯