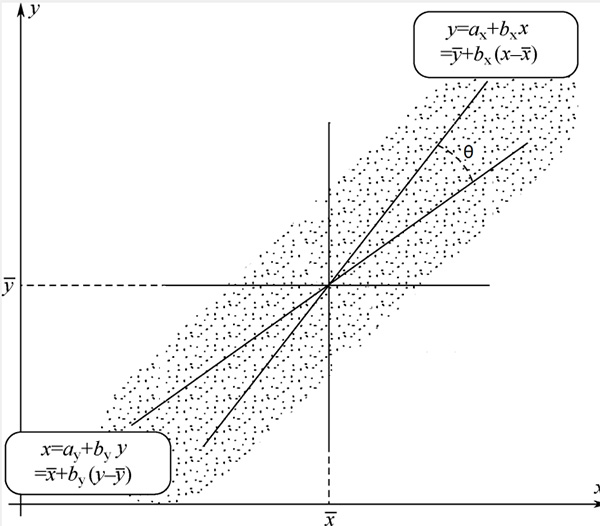
回归直线方程
回归直线方程指在一组具有相关关係的变数的数据(x与Y)间,一条最好地反映x与y之间的关係直线。
离差作为表示Xi对应的回归直线纵坐标y与观察值Yi的差,其几何意义可用点与其在回归直线竖直方向上的投影间的距离来描述。数学表达:Yi-y^=Yi-a-bXi.
总离差不能用n个离差之和来表示,通常是用离差的平方和,即(Yi-a-bXi)^2计算。
基本介绍
- 中文名:回归直线方程
- 外文名:Linear regression equation
- 别称:回归方程
- 套用学科:数学
- 适用领域範围:数理计算
- 适用领域範围:计算
定义
若:在一组具有相关关係的变数的数据(x与Y)间,通过散点图我们可观察出所有数据点都分布在一条直线附近,这样的直线可以画出许多条,而我们希望其中的一条最好地反映x与Y之间的关係,即我们要找出一条直线,使这条直线“最贴近”已知的数据点,记此直线方程为(如右所示,记为①式)这里在y的上方加记号“^”,是为了区分Y的实际值y,表示当x取值Xi=1,2,……,6)时,Y相应的观察值为Yi,而直线上对应于Yi的纵坐标是 ①式叫做Y对x的回归直线方程,相应的直线叫做回归直线,b叫做回归係数。 ①式
①式
 ①式
①式计算方法
要确定回归直线方程①,只要确定a与回归係数b。回归直线的求法通常是最小二乘法:离差作为表示xi对应的回归直线纵坐标y与观察值yi的差,其几何意义可用点与其在回归直线竖直方向上的投影间的距离来描述。数学表达:Yi-y^=Yi-a-bXi.总离差不能用n个离差之和来表示,通常是用离差的平方和即(Yi-a-bXi)^2计算。即作为总离差,并使之达到最小,这样回归直线就是所有直线中除去最小值的那一条。这种使“离差平方和最小”的方法,叫做最小二乘法。用最小二乘法求回归直线方程中的a,b有图一和图二所示的公式进行参考。其中,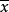 和
和 如图三所示,且
如图三所示,且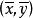 称为样本点的中心。
称为样本点的中心。



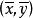



 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯