多重线性回归
多重线性回归(multiple linear regression) 是简单直线回归的推广,研究一个因变数与多个自变数之间的数量依存关係。多重线性回归用回归方程描述一个因变数与多个自变数的依存关係,简称多重回归。
基本介绍
- 中文名:多重线性回归
- 外文名:multiple linear regression
- 简称:多重回归
- 所属学科:数学
- 相关概念:偏回归係数,残差,多重共线性等
基本信息
多重线性回归的数学模型为:
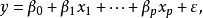
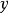
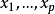
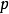

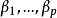
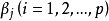
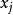

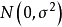
由样本估计的多重线性回归方程为:
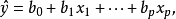
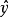
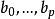
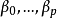
不能直接用各自变数的普通偏回归係数的数值大小来比较方程中它们对因变数y的贡献大小,因为p个自变数的计量单位及变异度不同。可将原始数据进行标準化,即
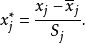
然后用标準化的数据进行回归模型拟合,此时获得的回归係数记为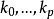 ,称为标準化偏回归係数(standardized partial regression coefficient ),又称为通径係数(pathcoefficient)。标準化偏回归係数
,称为标準化偏回归係数(standardized partial regression coefficient ),又称为通径係数(pathcoefficient)。标準化偏回归係数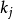 绝对值较大的自变数对因变数y的贡献大。
绝对值较大的自变数对因变数y的贡献大。
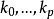
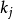
参数估计
多重线性回归分析中回归係数的估计也是通过最小二乘法(method of least square),即寻找适宜的係数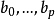 使得因变数残差平方和达到最小。其基本原理是: 利用观察或收集到的因变数和自变数的一组数据建立一个线性函式模型,使得这个模型的理论值与观察值之间的离均差平方和最小。
使得因变数残差平方和达到最小。其基本原理是: 利用观察或收集到的因变数和自变数的一组数据建立一个线性函式模型,使得这个模型的理论值与观察值之间的离均差平方和最小。
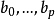
假设检验
建立的回归方程是否符合资料特点,以及能否恰当地反映因变数y与p个自变数的数量依存关係,就必须对该模型进行检验。
1.回归方程的检验与评价。无效假设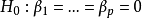 ;备择假设
;备择假设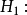 各
各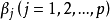 不全为0。检验统计量为F,计算公式为:
不全为0。检验统计量为F,计算公式为:
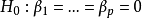
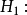
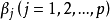
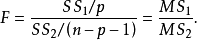
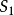
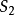
2.自变数的假设检验。
(1) 偏回归平方和检验。回归方程中某一自变数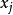 的偏回归平方和(sum of squaresfor partial regression),表示从模型中剔除
的偏回归平方和(sum of squaresfor partial regression),表示从模型中剔除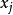 后引起的回归平方和的减少量。偏回归平方和用SS回归
后引起的回归平方和的减少量。偏回归平方和用SS回归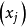 表示,其大小说明相应自变数的重要性。
表示,其大小说明相应自变数的重要性。
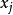
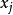
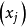
检验统计量F的计算公式为:
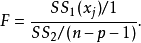
(2) 偏回归係数的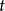 检验。偏回归係数的t检验是在回归方程具有统计学意义的情况下,检验某个总体偏回归係数是否等于0的假设检验,以判断相应的自变数是否对因变数y的变异确有贡献。
检验。偏回归係数的t检验是在回归方程具有统计学意义的情况下,检验某个总体偏回归係数是否等于0的假设检验,以判断相应的自变数是否对因变数y的变异确有贡献。
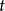
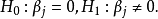
检验统计量t的计算公式为:
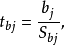
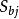
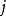
自变数的选择
在许多多重线性回归中,模型中包含的自变数没有办法事先确定,如果把一些不重要的或者对因变数影响很弱的变数引人模型,则会降低模型的精度。所以自变数的选择是必要的,其基本思路是: 儘可能将对因变数影响大的自变数选入回归方程中,并儘可能将对因变数影响小的自变数排除在外,即建立所谓的“最优”方程。
1.筛选标準与原则。对于自变数各种不同组合建立的回归模型,使用全局择优法选择“最优”的回归模型。
(1) 残差平方和缩小与决定係数增大。如果引人一个自变数后模型的残差平方和减少很多,那幺说明该自变数对因变数y贡献大,将其引入模型;反之,说明该自变数对因变数y贡献小,不应将其引入模型。另一方面,如果某一变数剔除后模型的残差平方和增加很多,则说明该自变数对因变数y贡献大,不应被剔除;反之,说明该自变数对因变数y贡献小,应被剔除。决定係数增大与残差平方和缩小完全等价。
(2) 残差均方缩小与调整决定係数增大。残差均方缩小的準则是在残差平方和缩小準则基础上增加了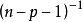 因子,它随模型中自变数p的增加而增加,体现出对模型中自变数个数增加所实施的惩罚。调整决定係数增大与残差均方缩小完全等价。
因子,它随模型中自变数p的增加而增加,体现出对模型中自变数个数增加所实施的惩罚。调整决定係数增大与残差均方缩小完全等价。
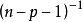
(3) 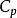 统计量。由C.L.Mallows提出,其定义为:
统计量。由C.L.Mallows提出,其定义为:
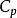
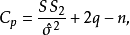
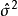
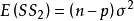
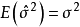
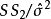
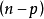
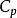
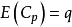
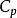

2.自变数筛选常用方法。常用方法如下:
(1) 前进法(forward selection)。事先定一个选人自变数的标準。开始时,方程中只含常数项,按自变数对y的贡献大小由大到小依次选入方程。每选入一个自变数,则要重新计算方程外各自变数(剔除已选人变数的影响后) 对y的贡献,直到方程外变数均达不到选入标準为止。变数一旦进人模型,就不会被剔除。
(2) 后退法(backward selection)。事先定一个剔除自变数的标準。开始时,方程中包含全部自变数,按自变数y对的贡献大小由小到大依次剔除。每剔除一个变数,则重新计算未被剔除的各变数对y的贡献大小,直到方程中所有变数均不符合剔除标準,没有变数可被剔除为止。自变数一旦被剔除,则不考虑进入模型。
(3) 逐步回归法(stepwise selection)。本法区别于前进法的根本之处是每引人一个自变数,都会对已在方程中的变数进行检验,对符合剔除标準的变数要逐一剔除。
解决方案
多重共线性(multi-colinearity) 是进行多重回归分析时存在的一个普遍问题。多重共线性是指自变数之间存在近似的线性关係,即某个自变数能近似地用其他自变数的线性函式来表示。在实际回归分析套用中,自变数间完全独立很难,所以共线性的问题并不少见。自变数一般程度上的相关不会对回归结果造成严重的影响,然而,当共线性趋势非常明显时,它就会对模型的拟合带来严重影响。
(1) 偏回归係数的估计值大小甚至是方向明显与常识不相符。
(2) 从专业角度看对因变数有影响的因素,却不能选入方程中。
(3) 去掉一两个记录或变数,方程的回归係数值发生剧烈的变化,非常不稳定。
(4) 整个模型的检验有统计学意义,而模型包含的所有自变数均无统计学意义。
当出现以上情况时,就需要考虑是不是变数之间存在多重共线性。
多重共线性的诊断
在做多重回归分析的共线性诊断时,首先要对所有变数进行标準化处理。SPSS中可以通过以下指标来辅助判断有无多重共线性存在。
(1) 相关係数。通过做自变数间的散点图观察或者计算相关係数判断,看是否有一些自变数间的相关係数很高。一般来说,2个自变数的相关係数超过0.9,对模型的影响很大,将会出现共线性引起的问题。这只能做初步的判断,并不全面。
(2) 容忍度(tolerance)。以每个自变数作为因变数对其他自变数进行回归分析时得到的残差比例,大小用1减去决定係数来表示。该指标值越小,则说明被其他自变数预测的精度越高,共线性可能越严重。
(3) 方差膨胀因子(variance inflation factor,VIF)。方差膨胀因子是容忍度的倒数,VIF越大,显示共线性越严重。VIF>10时,提示有严重的多重共线性存在。
(4) 特徵根(eigenvalue)。实际上是对自变数进行主成分分析,如果特徵根为0,则提示有严重的共线性。
(5) 条件指数(condition index)。当某些维度的该指标大于30时,则提示存在共线性。
共线性解决方案
自变数间确实存在多重共线性,直接採用多重回归得到的模型肯定是不可信的,此时可以用下面的办法解决。
(1) 增大样本含量,能部分解决多重共线性问题。
(2) 把多种自变数筛选的方法结合起来拟合模型。建立一个“最优”的逐步回归方程,但同时丢失一部分可利用的信息。
(3) 从专业知识出发进行判断,去除专业上认为次要的,或者是缺失值比较多、测量误差较大的共线性因子。
(4) 进行主成分分析,提取公因子代替原变数进行回归分析。
(5) 进行岭回归分析,可以有效解决多重共线性问题。
(6) 进行通径分析(path analysis),可以对应自变数间的複杂关係精细刻画。
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯