联合分布
联合分布函式(joint distribution function)亦称多维分布函式,随机向量的分布函式,以二维情形为例,若(X,Y)是二维随机向量,x、y是任意两个实数,则称二元函式。
基本介绍
- 中文名:联合分布
- 外文名:Joint distribution
- 套用领域:统计学
- 性质:分布
- 特点:联合
定义
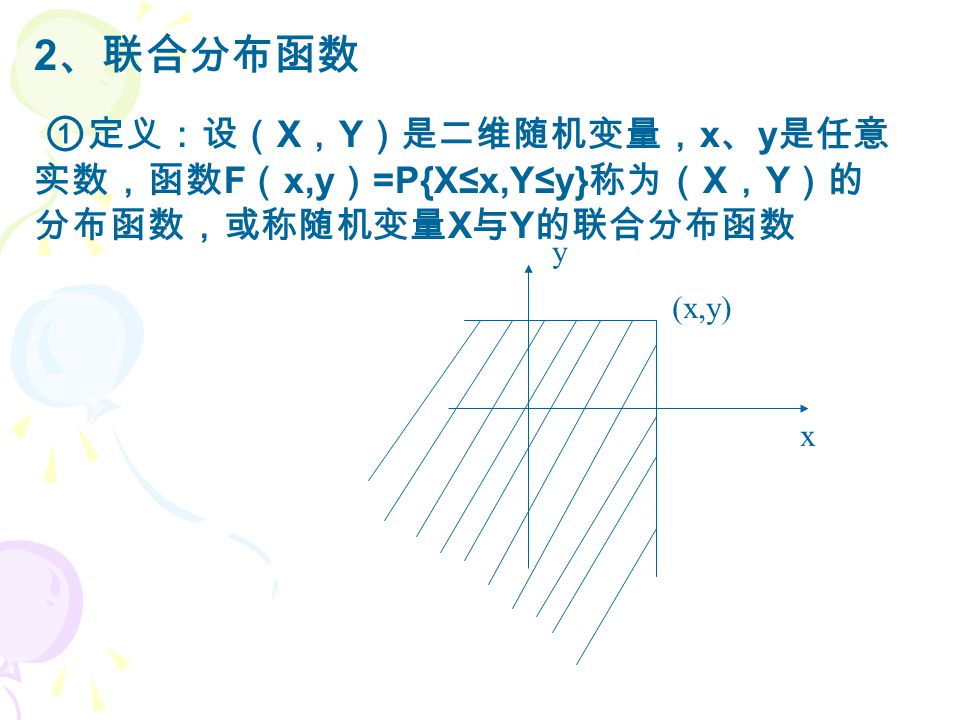
设(X,Y)是二维随机变数,对于任意实数x,y,二元函式:
F(x,y) = P{(X<=x) 交 (Y<=y)} => P(X<=x, Y<=y)
称为:二维随机变数(X,Y)的分布函式,或称为随机变数X和Y的联合分布函式。
随机变数X和Y的联合分布函式是设(X,Y)是二维随机变数,对于任意实数x,y,二元函式:F(x,y) = P{(X<=x) 交 (Y<=y)} => P(X<=x, Y<=y)称为二维随机变数(X,Y)的分布函式。
几何意义
联合机率分布的几何意义
如果将二维随机变数(X,Y)看成是平面上随机点的坐标,那幺分布函式F(x,y)在(x,y)处的函式值就是随机点(X,Y)落在以点(x,y)为顶点而位于该点左下方的无穷矩形域内的机率。
机率分布
在机率论中, 对两个随机变数X和Y,其联合分布是同时对于X和Y的机率分布。
二维变数
设E是一个随机试验,它的样本空间是S={e}。设X=X(e)和Y=Y(e)是定义在S上的随机变数,由它们构成的一个向量(X,Y),叫做二维随机向量或二维随机变数。
离散变数
对离散随机变数 X, Y 而言,联合分布机率密度函式如下:
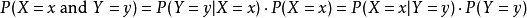
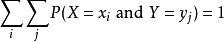
连续变数
类似地,对连续随机变数而言,联合分布机率密度函式为fX,Y(x, y),其中fY|X(y|x)和fX|Y(x|y)分别代表X = x时Y的条件分布以及Y = y时X的条件分布;fX(x)和fY(y)分别代表X和Y的边缘分布。
同样地,因为是机率分布函式,所以必须有:∫x∫y fX,Y(x,y) dy dx=1
独立变数
若对于任意x和y而言,有离散随机变数 :
P(X=x and Y=y)=P(X=x) ·P(Y=y)
或者有连续随机变数:
pX,Y(x,y)=pX(x)·pY(y)
则X和Y是独立的。
多元组合
二元联合分布可以推广到任意多元的情况X1, ..., Xn
fx1,…..,xn(x1,….,xn)=fxn∣x1,...,xn-1(xn∣x1,...,xn-1)fx1,...,xn-1(x1,...,xn-1)
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯