晶体学点群
在晶体学中,晶体学点群是对称操作(例如旋转、反映)的集合。这些操作以固定的中心向其他方向移动能使晶体复原,因此称为对称操作。对于一种真正的晶体(不是準晶体),点群对应的操作必须能够保持晶体的三维平移对称性。经过它的点群中任何操作之后,晶体的巨观性质依然和操作前完全相同[1]。在晶体的分类中,每一种点群也称为晶类。
这样看来似乎有无穷多种三维点群。然而,根据晶体局限定理可知,无穷多族的普通点群可以概括成32种晶体学点群。这32种点群与1830年约翰·弗里德里希·克里斯蒂安·赫塞尔提出的32种晶体形态学(外部)对称性是等价的,而他是从观察晶体外形得出的此结论。
基本介绍
- 中文名:晶体学点群
- 提出者:约翰·弗里德里希·克里斯蒂安·赫塞尔
- 提出时间:1830
- 套用学科:晶体学
释义
与晶体的32种对称元素系相对应的对称动作群。各种晶体的(理想)多面体外形会呈现出不同类型的对称性。这些晶体的对称性可用对称元素n重旋转和n重反组合成的各种对称元素系反映对应的最基本的对称动作是绕轴旋转360°/n紧接以一个倒反动作,倒反动作据以进行的点应在轴线上)。基于晶体内部是具有点阵式的三维周期性结构,可以证明,晶体中允许存在的对称轴的轴次n仅限于1、2、3、4、6,即晶体外形中可能呈现的对称元素只限旋转轴 和反轴 ,此中一重反轴即对称中心,二重反轴即镜面。晶体外形可能归属的对称类型共有32种,对应于32种对称元素系。 晶体学点群
晶体学点群 晶体学点群
晶体学点群
 晶体学点群
晶体学点群 晶体学点群
晶体学点群实验
由于32种对称元素系都至少有一个相交的公共点并各与一套能使晶体(理想)外形复原的点对称动作群(实行对称操作时,对称物体至少有一点是不动的动作,称为点对称动作)相对应,这32种对称元素系对应的对称动作群称做晶体学点群。 晶体学点群
晶体学点群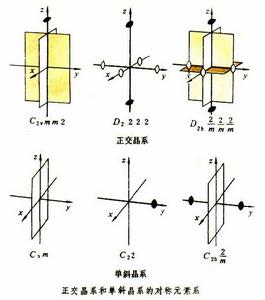 晶体学点群
晶体学点群
 晶体学点群
晶体学点群 晶体学点群
晶体学点群晶体在巨观观察中,在平行方向上呈现为具有均匀性的物体。由于结构中任何对称动作所包含的平移已被均匀性所掩盖,晶体结构中含平移的螺旋轴和滑移面在晶体巨观性质中将表现为相应的旋转轴和镜面。晶体巨观性质和晶体外形的对称类型均以晶体微观对称性为基础,也即晶体学点群以晶体学空间群为基础。
熊夫利记号中大写字母T、O、C、D、S代表四面体群、八面体群、双面群、反轴群等,小写字母i、s、v、h和d代表对称中心、镜面、通过主轴镜面、与主轴垂直镜面、等分两个副轴的镜面。单斜晶系一般取b为主轴,其他晶系一般取c为主轴。 晶体学点群
晶体在衍射效应中,若将比率极小的反常散射忽略不计,则衍射强度在三维空间中将呈现具有对称中心的对称性。这一实验现象称为夫里德耳定律。基于这一定律,晶体衍射强度分布的对称类型只能属于32个对称元素系中11个含对称中心者,与之对应的11个点群(即Ci、C2h、D2h、D3d、C3i、D6h、C6h、D4h、C4h、Th、Oh)称为劳厄点群。 晶体学点群
晶体学点群 晶体学点群
晶体学点群
 晶体学点群
晶体学点群 晶体学点群
晶体学点群记号
点群表示的是晶体所包含的对称元素。目前有多种不同的记号,分别由结晶学家、矿物学家、物理学家和化学家使用。
对于下面两种不同系统的关係,请参见晶系。
熊夫利记号
主条目:熊夫利记号
- 更多资料:三维点群
在熊夫利中,点群是用字母符号加上数字下标表示的。下面简述晶体学中使用的这种符号的意义:
- Cn(循环群)表示该群有一根n次旋转轴。Cnh是Cn加上一个与旋转轴垂直的镜面(反映)对称元素。Cnv则是Cn加上n个与旋转轴平行的镜面对称元素。
- S2n(源自德语Spiegel,意思是镜面)表示一根只含有2n次旋转反映轴(简称映轴)。
- Dn(二面体群)表示这个群只有一根n次旋转轴和n根垂直于这根主轴的二重轴。Dnh是加上一个与n次旋转轴垂直的镜面。Dnd则是Dn是加上n个与n次旋转轴平行的镜面。
- 字母T(四面体)表示这个群有四面体的对称性。Td则包括了旋转反映操作,T群本身则不包含旋转反映操作,Th则是T群加上与旋转轴垂直的镜面。
- 字母O(八面体)表示该群具有八面体或者立方体的对称性,可能包括(Oh)或不包括(O)旋转反映操作。
根据晶体局限定理,在二维或三维空间中n的取值只有1、2、3、4和6。
| n | 1 | 2 | 3 | 4 | 6 |
|---|---|---|---|---|---|
Cn | C1 | C2 | C3 | C4 | C6 |
Cnv | C1v=C1h | C2v | C3v | C4v | C6v |
Cnh | C1h | C2h | C3h | C4h | C6h |
Dn | D1=C2 | D2 | D3 | D4 | D6 |
Dnh | D1h=C2v | D2h | D3h | D4h | D6h |
Dnd | D1d=C2h | D2d | D3d | D4d | D6d |
S2n | S2 | S4 | S6 | S8 | S12 |
D4d和D6d实际上是不存在的,因为它们分别包含了n=8和12的旋转反映轴。表格中剩下的27种点群与T、Td、Th、O和Oh共同组成32种晶体学点群。
赫尔曼–莫甘记号
主条目:赫尔曼–莫甘记号
赫尔曼–莫甘记号的一种简略形式广泛用于表示空间群,也用于描述晶体学点群。群的名称列在下表中:
1 | 1 | |||||
2 | ⁄m | 222 | m | mm2 | mmm | |
3 | 3 | 32 | 3m | 3m | ||
4 | 4 | ⁄m | 422 | 4mm | 42m | ⁄mmm |
6 | 6 | ⁄m | 622 | 6mm | 62m | ⁄mmm |
23 | m3 | 432 | 43m | m3m |
对应关係
| 晶族 | 晶系 | 赫尔曼–莫甘 (完整记号) | 赫尔曼–莫甘 (简写记号) | 舒勃尼科夫 | 熊夫利 | 轨形记号 | 考克斯特记号 | 顺序 |
|---|---|---|---|---|---|---|---|---|
三斜 | 1 | 1 | C1 | 11 | [ ] | 1 | ||
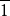 | 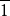 | Ci= S2 | x | [1,2] | 2 | |||
单斜 | 2 | 2 | C2 | 22 | [2] | 2 | ||
m | m | Cs= C1h | * | [ ] | 2 | |||
2/m | C2h | 2* | [2,2] | 4 | ||||
正交 | 222 | 222 | D2= V | 222 | [2,2] | 4 | ||
mm2 | mm2 | C2v | *22 | [2] | 4 | |||
mmm | D2h | *222 | [2,2] | 8 | ||||
四方 | 4 | 4 | C4 | 44 | [4] | 4 | ||
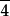 | 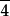 | S4 | 2x | [2,4] | 4 | |||
4/m | C4h | 4* | [2,4] | 8 | ||||
422 | 422 | D4 | 422 | [4,2] | 8 | |||
4mm | 4mm | C4v | *44 | [4] | 8 | |||
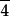 | 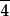 | D2d | 2*2 | [2,4] | 8 | |||
4/mmm | D4h | *422 | [4,2] | 16 | ||||
六方 | 三方 | 3 | 3 | C3 | 33 | [3] | 3 | |
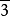 | 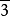 | S6= C3i | 3x | [2,6] | 6 | |||
32 | 32 | D3 | 322 | [3,2] | 6 | |||
3m | 3m | C3v | *33 | [3] | 6 | |||
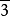 | 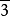 | D3d | 2*3 | [2,6] | 12 | |||
六方 | 6 | 6 | C6 | 66 | [6] | 6 | ||
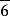 | 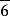 | C3h | 3* | [2,3] | 6 | |||
6/m | C6h | 6* | [2,6] | 12 | ||||
622 | 622 | D6 | 622 | [6,2] | 12 | |||
6mm | 6mm | C6v | *66 | [6] | 12 | |||
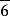 | 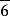 | D3h | *322 | [3,2] | 12 | |||
6/mmm | D6h | *622 | [6,2] | 24 | ||||
立方 | 23 | 23 | T | 332 | [3,3] | 12 | ||
3 | m3 | Th | 3*2 | [3,4] | 24 | |||
432 | 432 | O | 432 | [4,3] | 24 | |||
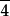 | 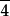 | Td | *332 | [3,3] | 24 | |||
3 | m3m | Oh | *432 | [4,3] | 48 | |||
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯