CSPs将其问题中的单元(entities)表示成在变数上有限条件的一组同质(homogeneous)的集合, 这类问题透过"约束补偿方法"来解决。CSPs是人工智慧和运筹学 的热门主题,因为它们公式中的规律，提供了共同基础来分析、解决很多看似不相关的问题。 CSPs通常呈现高複杂性, 需要同时透过启发式搜寻和联合搜寻 的方法，来在合理的时间内解决问题。 布尔可满足性问题 (SAT), 可满足性的理论 (SMT)和回答集程式设计 (ASP) 可以算是某种程度上的约束满足问题。

正式来说，约束满足问题定义为一个三元组 ，其中

是变数的集合,

是各个变数的定义域集合,而

是限制条件的集合。

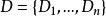
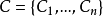
每个变数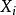 可以在非空的定义域 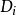中取出。每个限制条件(Constraint) 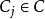依序对应一对 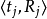，其中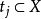 是 {\displaystyle n} n-tuple的变数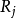， 则是在定义域 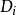中，其对应到的子集合上得到的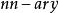维的关係。 变数的评估(evaluation)是一个函式，其从变数的子集合映射到一组特定的集合，集合内为定义域的子集合所对应到的值，也就是

如果，则此评估(evaluation) f满足条件限制 。

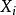
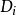
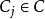
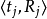
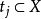
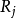
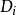
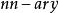
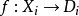
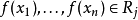
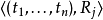
如果一个评估不违反任何的条件限制，我们说这个评估是无矛盾的(consistent)。 如果一个评估包含了所有的变数，我们说这个评估是完备的(complete)。 如果一个评估无矛盾而且完备的，我们说这个评估是一个解(solution)，这样的评估就会用来解决CSP。

定义域有限的约束满足问题通常利用搜寻方法来解决。最常用的技术是回溯法(backtracking)、约束传递constraint propagation，以及局部搜寻local search的改良。

回溯法 是一种递归算法，它保持部分变数的赋值。一开始，所有的变数都还没被赋值。在每一个步骤中，先选取一个变数，并且将所有可能的值依次赋予该变数。对于每一个值，在限制条件下的局部赋值的无矛盾性(consistency)都进行检查。在匹配无矛盾(consistency)的情况下，就会递归地往下调用。当所有的值都试过，算法则回溯上层。在这个基本回溯算法中，无矛盾性(consistency)被定义为满足所有的条件限制，且这些条件限制的变数已被赋值。若干回溯变数存在。 回溯法 提高了检查无矛盾性的效率。 回跳法 可以使在某些在某些情况中，透过回溯”一个以上的变数“，来省去部分的搜寻。 约束学习则藉由减少新的条件限制,来避免部分的搜寻。 可预见性也常常在回溯法中套用，用来去预期选择一个变数或值的影响，因此常常用来预先判定一个子问题什幺时候满足或不满足。 约束传递 (Constraint propagation)技术是用来修饰一个CSP的方法。更精确地说，是一种方法，用来增强一种形式的局部一致性，是一种条件牵连到一组变数或条件限制的一致性。约束传播套用在各个领域。一来,它把问题转化为一个等价但通常是最简单的解决方法。 二来，他可以用来验证满足或不满足于问题。 一般来说他不保证会发生，但是它总是会发生一些形式的约束传递(Constraint propagation)或某些种类的问题。 最有名的惯用的局部一致性是 弧协调性，超弧一致性，和路径一致性。 最流行的方法是AC-3约束传播算法，该算法可以运行弧的一致性。

局部搜寻方法 是不完全满足的算法。人们可能找到解决问题的方法， 但这方法可能令我们失望。其反覆更改变数来改进整个任务，而得以运作。在每一步，要更改少量变数的值,与整体目标数量的增加条件限制以满足的任务。 最小冲突算法是局部搜寻算法和基于特定CSPs原则。在实践中,局部搜寻似乎工作当这些变化也受随机选择。集成搜寻和局部搜寻被开发了,导致混合算法。

CSPs也研究计算複杂性问题和有限模型理论. 一个重要的问题是，是否为每一组的关係、套都可视为CSPs选自只使用关係设定不是在p 或 NP-完全问题. 如果这样一个二分法真实可靠， 那幺CSPs提供已知的最大的一个NP 子集,避免NP-intermediate 问题，其存在是证明了Ladner's 理论 在这种假定下 P ≠ NP. Schaefer's 二分法理论 处理所用变数相关时的情况布尔数学运算符, 也就是， 对一个定义域大小为2的。 最近的一个促进dichotomoy二分定理推广到一个更大的类的事务。

相同的情形存在于功能类别之间，FP 和 #P.通过一般的Ladner's 理论, FP 和 #P-complete 也存在问题如果 FP ≠ #P。在这种决策下， 一个#CSP问题被定义为一组关係。每个问题需要输入布尔 公式作为输入，任务是计算数字令人满意的工作。这可以进一步推广利用大域大小和附上一个权重，对每一个满意的赋值和计算这些权值的总和。 众所周知任何複杂的#CSP权重问题既不是FP 也不是 #P-hard问题。

动态CSPs (DCSPs) 是有用的，当原有的问题形式以某种方式改变，通常是由于约束集进化，因为要考虑环境。DCSPs被当做一系列的静态CSPs，每一个都是转变的前一个变数和约束可以添加或删除限制(放鬆)。信息在初始的配方发现问题可以用来提炼下一个。解决的方法可分为根据信息的方法在转让:

经典的CSPs处理约束很严格，意味着强制的 (每一解决方案必须满足所有问题) 并且刻板的 (意味着,以至于他们必须被完全满足,否则他们是完全违反了)。 灵活的 CSPs 放宽假设, 部分的放宽限制对不遵循的的也一样解决问题。 这类似于preference-based planning. 一些类型的灵活 CSPs 包括: