乌雷松非线性积分运算元
乌雷松非线性积分运算元是一类相当广泛的非线性积分运算元。这类运算元是由乌雷松于1924年首先提出并加以研究的。
基本介绍
- 中文名:乌雷松非线性积分运算元
- 外文名:Urysohn nonlinearintegral operator
- 适用範围:数理科学
简介
乌雷松非线性积分运算元是一类相当广泛的非线性积分运算元。
设k(x,y,u):G×G×R1→R1是可测函式,则形如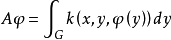 的运算元称为乌雷松非线性积分运算元。
的运算元称为乌雷松非线性积分运算元。
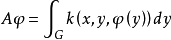
性质
全连续性是非线性积分运算元的重要性质。
如果k(x,y,u)在G×G×R1上连续,则乌雷松非线性积分运算元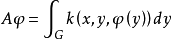 是作用在C(G)上的全连续运算元。
是作用在C(G)上的全连续运算元。
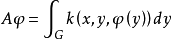
进一步,下列结果成立:若G是具有非零测度的有界闭集,对一切x∈G,和几乎一切y∈G,k(x,y,u)关于u连续,并且对一切x∈G,u∈R1,k(x,y,u)关于y可测,则相应的乌雷松非线性积分运算元映C(G)入自身全连续的充分必要条件是,对任给a>0,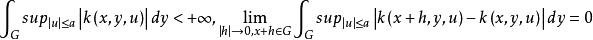 对一切x∈G成立。
对一切x∈G成立。
发展
乌雷松非线性积分运算元是一类很广泛的运算元类,包含了哈默斯坦非线性积分运算元和沃尔泰拉非线性积分运算元作为特殊情况。这类运算元由于过于广泛,研究起来困难很大,所以到目前为止,除了在该类运算元的全连续判别上有了较系统的结果之外,关于乌雷松非线性积分方程解的性质的研究,结果是很少的,还有待于人们去探索。
这类运算元是由乌雷松于1924年首先提出并加以研究的。
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯