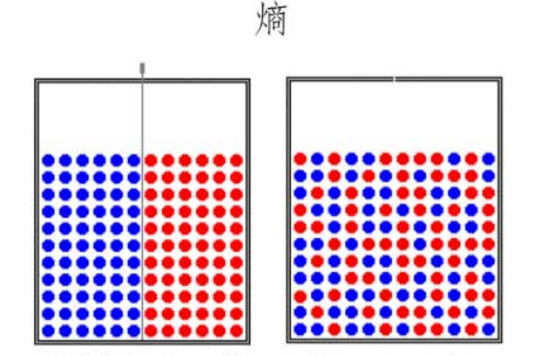
熵(统计物理与资讯理论术语)
熵的概念是由德国物理学家克劳修斯于1865年所提出。最初是用来描述“能量退化”的物质状态参数之一,在热力学中有广泛的套用。但那时熵仅仅是一个可以通过热量改变来测定的物理量,其本质仍没有很好的解释,直到统计物理、资讯理论等一系列科学理论发展,熵的本质才逐渐被解释清楚,即,熵的本质是一个系统“内在的混乱程度”。它在控制论、机率论、数论、天体物理、生命科学等领域都有重要套用,在不同的学科中也有引申出的更为具体的定义,按照数理思维从本质上说,这些具体的引申定义都是相互统一的,熵在这些领域都是十分重要的参量。
基本介绍
- 中文名:熵
- 外文名:entropy
- 提出人:克劳修斯
- 提出时间:1865年
熵概念的提出
熵(希腊语:entropia 英语:entropy)的概念是由德国物理学家克劳修斯于1865年所提出。在希腊语源中意为“内在”,即“一个系统内在性质的改变”,公式中一般记为S。1923年,德国科学家普朗克(Plank)来中国讲学用到entropy这个词,胡刚复教授翻译时灵机一动,把“商”字加火旁来意译“entropy”这个字,创造了“熵”字,(读shāng),因为熵变dS是dQ除以T(温度)的商数。
克劳修斯将一个热力学系统中熵的改变定义为:在一个可逆过程中,输入热量相对于温度的变化率,即
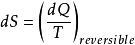
首先这里解释一下什幺是“可逆过程”。热力学过程是指一个系统热力学性质的改变过程,例如温度、体积、压强、内能等。当一个过程被界定为“可逆”时,即指改变过程在的每一个极短的步骤内,系统都保持非常接近平衡的状态,称为“準静态过程”。否则,该过程即是“不可逆的”。例如,在一个活塞管中的气体,其体积可以因为活塞移动而改变。“可逆”体积改变是指在进行得极其慢的步骤中,气体的密度一直保持均匀。“不可逆”体积改变即是指在快速的体积改变中,由于体积改变太快,可以形成密度梯度和压力波,并造成不稳定状态。无耗散的“準静态过程”即是“可逆过程”。若过程是不可逆的,则 不可逆。这里过程的“可逆性”涉及到一个和“熵”密切相关的物理原理,称为“熵增原理”,也就是“热力学第二定律”。热力学第二定律有很多表述形式,例如:①热量总是从高温物体传到低温物体,不可能作相反的传递而不引起其他的变化;②功可以全部转化为热(例如物体间摩擦使一部分机械能不可逆地转变为热),但任何热机不能全部地,连续不断地把所接受的热量转变为功(即无法製造第二类永动机);③在孤立系统中,实际发生过程,总使整个系统的熵值趋于增大。
不可逆。这里过程的“可逆性”涉及到一个和“熵”密切相关的物理原理,称为“熵增原理”,也就是“热力学第二定律”。热力学第二定律有很多表述形式,例如:①热量总是从高温物体传到低温物体,不可能作相反的传递而不引起其他的变化;②功可以全部转化为热(例如物体间摩擦使一部分机械能不可逆地转变为热),但任何热机不能全部地,连续不断地把所接受的热量转变为功(即无法製造第二类永动机);③在孤立系统中,实际发生过程,总使整个系统的熵值趋于增大。

这些不同表述各有侧重,但彼此等价。例如:在一个孤立系统中有两个温度不同的物体,热量dQ 由高温(T1)物体传至低温(T2)物体,高温物体的熵减少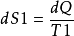 ,低温物体的熵增加
,低温物体的熵增加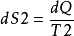 ,把两个物体合起来当成一个系统来看,熵的变化是dS=dS2-dS1>0,即熵是增加的。这说明了表述①和表述③的等价性。
,把两个物体合起来当成一个系统来看,熵的变化是dS=dS2-dS1>0,即熵是增加的。这说明了表述①和表述③的等价性。
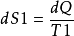
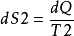
物理解释
1877年左右,玻尔兹曼提出熵的统计物理学解释。他在一系列论文中证明了:系统的巨观物理性质,可以认为是所有可能微观状态的等机率统计平均值。例如,考虑一个容器内的理想气体。微观状态可以用每个气体原子的位置及动量予以表达。所有可能的微观状态必须满足以下条件:(i)所有粒子的位置皆在容器的体积範围内;(ii)所有原子的动能总和等于该气体的总能量值。
玻尔兹曼提出一个系统的熵和所有可能微观状态的数目满足以下简单关係,

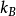
根据这个公式,我们可以将熵看作是一个系统“混乱程度”的度量,因为一个系统越混乱,可以看作是微观状态分布越均匀。例如,构想有一组10个硬币,每一个硬币有两面,掷硬币时得到最有规律的状态是10个都是正面或10个都是反面,这两种状态都只有一种构型(排列)。反之,如果是最混乱的情况,有5个正面5个反面,排列构型可以有排列组合数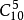 ,共252种。
,共252种。
根据熵的统计学定义,热力学第二定律说明一个孤立系统的倾向于增加混乱程度,根据上述硬币的例子可以明白,每一分钟我们随便掷一个硬币,经过一段长时间后,我们检查一下硬币,有“可能”10个都是正面或都是反面,但是最大的可能性是正面和反面的数量相等。
我们发现,混乱程度倾向于增加的观念被许多人接受,但容易引起一些错误认识,最主要的是必须明白ΔS ≥ 0只能用于“孤立”系统,值得注意的是地球并不是一个孤立系统,因为地球不断地从太阳以太阳光的形式接收能量。但有人认为宇宙是一个孤立系统,即宇宙的混乱程度在不断地增加,可以推测出宇宙最终将达到“热寂”状态,因为(所有恆星)都在以同样方式放散热能,能源将会枯竭,再没有任何可以作功的能源了。当然”宇宙是一个孤立系统“严格来说只是个未被验证的假设。
可以严格证明,玻尔兹曼公式的另一种等价表述形式是
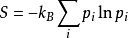
其中i标记所有可能的微观态,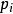 表示微观态i的出现几率。
表示微观态i的出现几率。
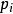
资讯理论解释
1948年,香农将统计物理中熵的概念,引申到信道通信的过程中,从而开创了”资讯理论“这门学科。香农定义的“熵”又被称为“香农熵” 或 “信息熵”, 即
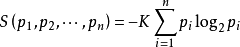
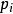
连续性
该度量应该是连续的,即,若样本机率值有微小变化,由此引起的熵变化也是微小的。
对称性
样本重新排序后,该度量应保持不变,即

极值性
当所有样本等几率出现的情况下,熵达到最大值(所有可能的事件等机率时不确定性最高)
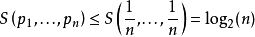
对于样本等几率分布而言,样本数越大,熵值越大(可能的时间越多,不确定性越高)
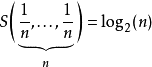
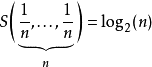
可加性
熵的值与过程如何被划分无关。它描述了一个系统与其子系统熵的关係。如果子系统之间的相互作用是已知的,则可以通过子系统的熵来计算一个系统的熵。例如:给定一个有n个样本的均匀分布集合,分为k个箱子(子系统),每个里面有 b1, ..., bk 个样本,合起来的熵应等于系统的熵与各个箱子的熵的和,每个箱子的权重为在该箱中样本的总机率。即,对于正整数bi其中b1 + ... + bk = n来说,
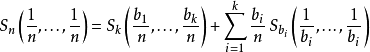
事实上,香农证明如果要求度量满足这些性质,则可以完全确定“信息熵”的定义表达式。
热力学熵
根据Jaynes(1957)的观点,热力学熵可以被视为香农信息理论的一个套用(这从玻尔兹曼公式和信息熵的定义相似性明显可以看出。):热力学熵被定义为与要进一步确定系统的微观状态所需要的更多香农信息的量成比例。比如,系统温度的上升提高了系统的热力学熵,这增加了系统可能存在的微观状态的数量,也意味着需要更多的信息来描述对系统的完整状态。
麦克斯韦在以他的名字命名的思想实验(“麦克斯韦妖”)中认为,如果存在一个小妖精知道每个分子的状态信息(热,或者冷),就能够降低系统的热力学熵。Landauer和他的同事则反驳说,让小妖精行使职责本身——即便只是了解和储存每个分子最初的香农信息——就会给系统带来热力学熵的增加,因此总的来说,系统的熵的总量没有减少。这就解决了“麦克斯韦妖”引发的悖论。Landauer法则能够解释现代计算机在处理大量信息时,必须解决散热问题。
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯