特徵价格法
特徵价格法,又称Hedonic模型法和效用估价法,认为房地产由众多不同的特徵组成,而房地产价格是由所有特徵带给人们的效用决定的。由于各特徵的数量及组合方式不同,使得房地产的价格产生差异。因此,如能将房地产的价格影响因素分解,求出各影响因素所隐含的价格,在控制地产的特徵(或品质)数量固定不变时,就能将房地产价格变动的品质因素拆离,以反映纯粹价格的变化。
特徵价格法的理论基础
特徵价格法的基本思路是:将房地产商品的价格分解,以显现出其各项特徵的隐含价格,在保持房地产的特徵不变的情况下,将房地产价格变动中的特徵因素分解,从价格的总变动中逐项剔除特徵变动的影响,剩下的便是纯粹由供求关係引起的价格变动。
特徵价格法:该理论认为,一种多样性商品具有多方面的不同特徵或品质(如房地产商品的面积、楼层、朝向和是否有保全服务等特徵),商品价格则是所有这些特徵的综合反映和表现。当商品某一方面的特徵改变时,商品的价格也会随之改变。
当商品的某一方面的特徵改变时,其价格也会随之发生改变。对函式的各个特徵变数分别求偏导数,就取得各特徵的变动对商品价格的影响幅度,并假定这种影响的关係在一定的时间内固定不变。这样,在缺乏同质商品的情况下,可以用非同质的房地产在基期与报告期之间进行比较,从价格的总变动中逐项剔除特徵变动的影响,最后剩下的便是纯粹由供求关係引起的价格变动了,这样计算的价格指数便是基于特徵价格法的房地产价格指数。
根据这一理论,房地产价格与各特徵因素之间的关係可以表示为: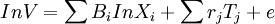
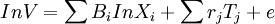
式中:
V:房价;
Xi :房屋的品质(特徵)因素;
Bi :各房屋的品质与房价关係的係数;
Tj :房屋在j期售出的哑元变数,即在j期出售,则Tj = 1 ,否则,Tj = 0 ;
rj :在j期售出的房屋的价格变动係数;
e:随机误差变数。
通过回归分析,可以得出各期的r值,并编制出房地产价格指数。
特徵价格模型的优缺点
特徵价格模型的优点是:容易取样,可以得到大量价格资料;模型的经济意义比较直观;计算相对简单。但同时,运用特徵价格法编制价格指数也存在多重共线性问题和因房地产的个别性而掩盖市场供求关係对房地产价格的影响等问题。
特徵价格法的主要形式
1.时间哑元法
其基本思路是,利用基期和多个报告期的样本建立统一的特徵价格模型,并在模型中以时间哑元变数标识样本所属的报告期,即: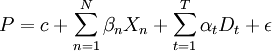

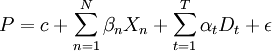

2.特徵价格指数法
其基本思路是,各个报告期分别建立特徵价格模型,以计算各住房特徵在各报告期内的特徵价格值,再选定一定的“标準单元”(即固定各住房特徵在各报告期内的取值)。将计算得到的特徵价格值和设定的标準单元值分别代入(2)后,即可得到“标準单元”在各报告期的同质价格,并以此为基础进行指数编制。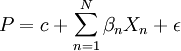
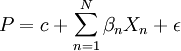
3.模拟价格法
模拟价格法是基于特徵价格模型对样本匹配法的改进。样本匹配法是普通商品价格统计中的一种常用方法,其基本思路是严格控制考察样本在各报告期内一致,以满足同质可比的要求。但由于住房具有高度异质性特点,同一住房单元几乎不可能在各报告期内均发生交易,而各期交易的住房单元在质量上又存在不可忽略的差异,因此传统的样本匹配法不能简单套用到住房价格指数编制过程中。
模拟价格法对样本匹配法的改进思路是,计算第t期指数时,首先利用第t-1期的特徵价格模型,推测第t期交易的住房单元(相当于第t期的“新增单元”)在第t-1期的价格,再利用第t期的特徵价格模型,推测第t-1期交易的住房单元(相当于第t期的“退出单元”)在第t期的价格,从而实现第t-1期和第t期内住房单元的完全匹配,进而引入传统的样本匹配法进行指数计算。
4.价格调整法
价格调整法同样是利用特徵价格模型对样本匹配法进行的一种改进。其基本思路是,确定某一虚拟的“标準住房单元”作为匹配样本,在各报告期内,均利用当期的特徵价格模型,将所有交易的住房单元的价格调整到统一的“标準住房单元”的基础上,再利用样本匹配法进行指数编制。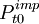
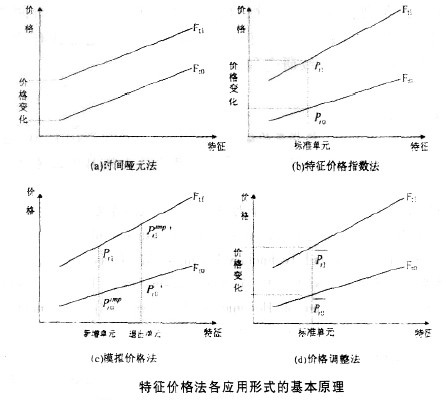
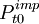

特徵价格法具体形式的选择
由于基本思路的差异,不同形式的特徵价格法各有其利弊和适用範围,这也使得具体形式的选择成为特徵价格法套用中的首要问题。
首先是直接特徵价格法和间接特徵价格法的选择。在住房价格指数编制中,间接特徵价格法需要对各住房单元逐一进行模拟或调整,因此相比之下间接特徵价格法的计算量明显超过直接特徵价格法,但结果的準确程度反而可能更低,从效果上看并非理想选择。因此,直接特徵价格法目前占据了主流地位,而间接特徵价格法的套用则主要限于对正在使用的非同质方法进行改进,例如德国统计部门正在进行的基于价格模拟法的住房价格指数编制研究等。
就直接特徵价格法而言,时间哑元法和特徵价格指数法也各有其显着特点。时间哑元法在特徵价格法的各种形式中计算最为简便,且通过多期样本的叠加,能够有效的避免样本代表性误差,其指数结果具有较好的稳健性。但如前所述,时间哑元法的前提假设是各住房特徵的特徵价格在各报告期内保持不变,当考察期延长,或当市场处于剧烈变化过程中时,这一假设很有可能无法成立,并将因此造成误差;其次,时间哑元法在进行指数更新时存在一定的困难,引入新的报告期时,估计得到的特徵价格模型将发生改变,并使历史指数值也发生变化。特徵价格指数法则可以有效的改善时间哑元法的这两方面不足,但该方法的稳健性较差,各报告期中的特徵价格估计值容易由于交易结构波动、样本容量不足或数据质量的微小误差而出现较大幅度的变化,并因而造成指数序列的震荡。由此可见,这两种方法不存在绝对的优劣之分,而适用于不同的市场情况。
另一种可行的思路是将时间哑元法和特徵价格指数法相结合,取长补短。目前较为常见的是链式指数法,这种方法仍以式(1)为基本形式,但在计算第t期价格指数时,仅引入第t期和第t-1期的样本,再通过时间哑元变数係数计算第t期价格指数相对于第t-1期的变化程度(即环比值),最后利用第t-1期价格指数和该环比值推算第t期价格指数。链式指数法同样有效的避免了时间哑元法存在的两方面缺陷,同时与特徵价格指数法相比,它通过两期样本的叠加,在一定程度上提高了结果的稳健性。在此基础上,对其进行了进一步发展,提出了扩展的链式指数法,在结果的稳健性程度等方面又有所提高。
特徵价格法的套用建议
特徵价格法的各种形式各有其优缺点和适用範围,因而可能在不同条件下套用于我国住房价格指数的编制。目前简单加权平均法和样本匹配法仍是我国住房价格指数编制中採用的主要方法,但这些非同质方法和近似同质方法的局限性已经日益显现出来,许多指数编制机构都在着手对此类指数进行升级。这种情况下,间接特徵价格法—— 尤其是其中的价格调整法可以成为一种理想选择,即以特徵价格模型取代人为设定的调整係数或调整公式,对不同住房单元在区位、楼层等主要特徵上存在的差异进行修正,再延用简单加权平均法或样本匹配法进行指数计算。这种方法可以在保持目前编制方法主体不变的基础上,以较小的成本实现指数结果同质化程度的明显提高。
但对于刚刚开始编制的住房价格指数而言,则没有必要採用间接特徵价格法,而可以直接引入计算更为简便、结果精度更高的直接特徵价格法。在时间哑元法和特徵价格指数法的选择中,从目前我国的实际情况看,住房市场处于快速发展的过程中,各种住房的特徵价格一直在发生变化,因此传统的时间哑元法并非理想选择。但与此同时,各报告期内交易的住房单元的波动同样十分明显,这又制约了特徵价格指数法的套用,特别是当城市的市场规模较小,或者报告期较短(例如指数逐月更新)时,指数结果的震荡将非常明显,足以掩盖真正有价值的价格信号。在这种情况下,综合两者优点的链式指数法和扩展链式指数法更有可能得到有效的套用,应当成为后续研究和套用的主要方向。
相关条目
房地产价格指数
成本投放法
中位数价格法
重複交易法
Pooled GLS模型
Pooled MLE模型
参考文献
1 吴璟 郑思齐 刘洪玉.编制住房价格指数的特徵价格法细解.统计与决策.2007 年第24期(总第252期)
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯