
状态函式
状态函式(state function),即指表征体系特性的巨观性质,多数指具有能量量纲的热力学函式(如内能、焓、吉布斯自由能、亥姆霍茨自由能)。主要套用于工程领域。
状态函式只对平衡状态的体系有确定值,其变化值只取决于系统的始态和终态。另外,状态函式之间相互关联、相互制约。
状态函式按其性质可分为两类,即广度性质和强度性质,其区别在于是否与物质的量有关。
基本介绍
- 中文名:状态函式
- 外文名:state function
- 含义:表征体系特性的巨观性质
- 实例:内能、焓、吉布斯自由能
- 领域:工程
- 分类:广度性质和强度性质
概念
在一定的条件下,系统的性质不再随时间而变化,其状态就是确定的,系统状态的一系列表征系统的物理量被称为状态函式(state function)。有时候也被称作热力学势,但“热力学势”更多的时候是特指内能、焓、吉布斯自由能、亥姆霍茨自由能等四个具有能量量纲的热力学函式。
状态函式表征和确定体系状态的巨观性质。状态函式只对平衡状态的体系有确定值,对于非平衡状态的体系则无确定值。在求各种热力学函式时,通常需要作路径积分(path integral),若积分结果与路径无关,该函式称为状态函式,否则即称为非状态函式。
若定义体系的一个性质A,在状态1,A有值A1;在状态2,有值A2,不管实现从1到2的途径如何,A在两状态之间的差值dA≡A2-A1恆成立,则A即称为状态函式。例如:温度、压力、体积、密度、能量、形态等,还有热力学函式:U(内能)、H(焓)、G(吉布斯函式)、F(自由能)、S(熵)等可以定义为体系的一个与路径无关的性质,而功和热则不可以,因为功和热无法与体系的特定状态联繫在一起。
介绍
体系一切巨观性质(化学性质和物理性质)的综合表现就是状态。这就是说,热力学是用体系的巨观性质来确定它的状态的。所以当体系各 种巨观性质都确定后,体系就应有确定的状态。反过来讲,体系的状态确定后, 各种巨观性质也就都有确定的数值。因此,体系的各种巨观性质应当是它所处 状态的单值函式。所以热力学把各种巨观性质都称为状态函式。这些巨观性质 随着状态的确定而确定,随着状态的变化而变化。
状态函式是由系统 的状态决定的性质。当状态一定,状态函式的数值也一定,如果状态发生变化,则相应的状态函式的变化值仅与系统的初态与 终态有关,而不问在此初终态间所经历的 具体过程如何。温度、压力、体积、内能等都是状态函式。例如,系统由1.01325×10帕273K变为3.03975×10帕298K,压 力变化即为2.02650×10帕,温度变化即 为25K,与如何变化的具体过程无关。状态函式的微分必定是全微分。
特徵
1、状态函式的变化值只取决于系统的始态和终态,与中间变化过程无关;并非所有的状态函式都是独立的,有些是相互关联、相互制约的,例如:对于普通的 温度-体积 热力学体系,p(压强)、V(体积)、T(温度)、n(物质的量)四个只有三个是独立的,p与V相互之间常有状态方程f(p,V)=0相关联(如理想气体中pV=nRT)。
2、状态函式的微变dX为全微分。全微分的积分与积分路径无关。利用这两个特徵,可判断某函式是否为状态函式。
3、具有单值性。
4、.状态函式的集合(和、差、积、商)也是状态函式。
分类
状态函式按其性质可分为两类:
一类是容量性质(又称广度性质)。在一定条件下,这类性质的量只与体系中所含物质的量成正比关係,具有加和性。如质量、体积、内能等。
另一类是强度性质,其量值与系统中物质的量无关,不具有加和性,仅决定于系统本身的特性。如密度、温度等。
简单系统
简单热力学系统一般具有以下状态函式,可以任意选取其中两个作为独立变数:
量纲(单位)不是能量的热力学函式
| 物理量 | 符号 | 单位 |
|---|---|---|
体积 | V | 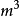 |
压强 | P | Pa和atm |
温度 | T | K和℃ |
熵 | S | J/(mol·K) |
量纲(单位)是能量的热力学势
| 物理量 | 符号 | 单位 |
|---|---|---|
内能 | U | J |
焓 | H | J |
吉布斯自由能 | G | J |
亥姆霍兹自由能 | F | J |
热力学势
在热力学函式中,后四个具有能量的量纲,单位都为焦耳,这四个量通常称为热力学势。
内能U 有时也用E表示
亥姆霍兹自由能A = U − TS 也常用F表示
焓 H = U + PV
吉布斯自由能 G = U + PV − TS
其中,T =温度, S =熵, P =压强, V =体积
分别选取T,S,P,V中的两个为自变数,它们的微分表达式为:
dU = TdS - PdV
dF = - SdT - PdV
dH = TdS + VdP
dG = - SdT + VdP
通过对以上微分表达式求偏导(偏导数),可以得到T,S,P,V四个变数的偏导数间的“麦氏关係”。
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯