
狄利克雷问题
在数学中,狄利克雷边界条件,为常微分方程的“第一类边界条件”,指定微分方程的解在边界处的值。求出这样的方程的解的问题被称为狄利克雷问题。狄利克雷问题(Dirichlet's problem)亦称第一边值问题,是调和函式的一类重要边值问题。求一个在区域D内调和并在(DU∂D)上连续的函式 u(z)的问题,要求它在∂D上取给定的连续函式φ(ξ)(ξ∈∂D)。
基本介绍
- 中文名:狄利克雷问题
- 外文名:Dirichlet's problem
- 别称:第一边值问题
- 类别:是调和函式的一类重要边值问题
- 一级学科:数学
- 二级学科:调和函式
简介
全体调和函式的总体,是拉普拉斯方程

这类条件中最简单的那一种,归结为在区域的边界的每一点上给定所求的调和函式的值。由此,产生了所谓第一边值问题,或者,狄利克雷问题:
求出一个在区域D内调和并且在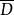 内连续的函式u(z),使它在D的边界上取已经给定的连续值u(ξ)。
内连续的函式u(z),使它在D的边界上取已经给定的连续值u(ξ)。
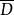
举例
例如,在某一区域内求热场的温度或静电场的势能,当在这区域的边界上的温度或势能已经知道时,便可化为狄利克雷问题。
在套用中,边界值u(ξ)是连续的这个条件,是限制过严了,所以需要考虑广义狄利克雷问题:
设已经在区域D的边界C上给出了一个函式u(ξ),它出了在有限多个点ξ1,ξ2,…,ξn处有第一类间断点外,是处处连续的。要求找出一个在区域D内的有界调和函式u(z),使它在函式u(ξ)的所有连续点处都取值u(ξ)**。
椭圆型方程的狄利克雷问题
求二阶椭圆型方程在区域边界上的值为已知的解。设区域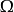 的边界为
的边界为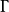 。求在
。求在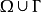 上连续、在
上连续、在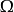 内满足给定的椭圆型方程、在
内满足给定的椭圆型方程、在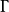 上取给定的连续边界值的解的问题,称为椭圆型方程的狄利克雷问题。
上取给定的连续边界值的解的问题,称为椭圆型方程的狄利克雷问题。
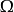
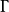
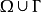
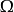
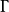
特别地,对有界区域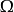 ,如果边界点都是正则点(参见“闸函式”),调和方程△u=0的狄利克雷问题的解存在且位移。
,如果边界点都是正则点(参见“闸函式”),调和方程△u=0的狄利克雷问题的解存在且位移。
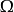
对于一般的强椭圆型方程
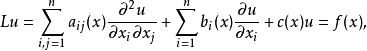
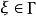

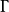
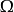
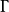
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯